Алгебра, вопрос задал kamenkovaanastasia36 , 11 месяцев назад

Допоможіть будь ласка з алгеброю

Приложения:

Ответы на вопрос

Ответил математик2011

Ответ:

на фото

Объяснение:

Приложения:

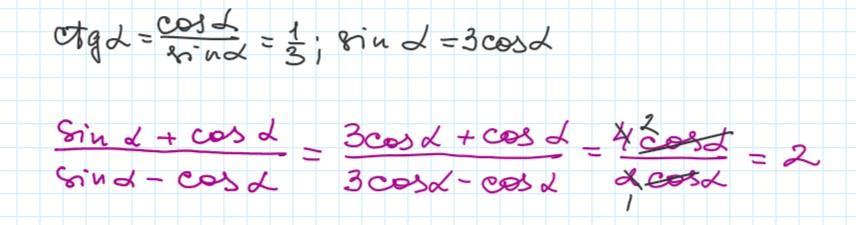
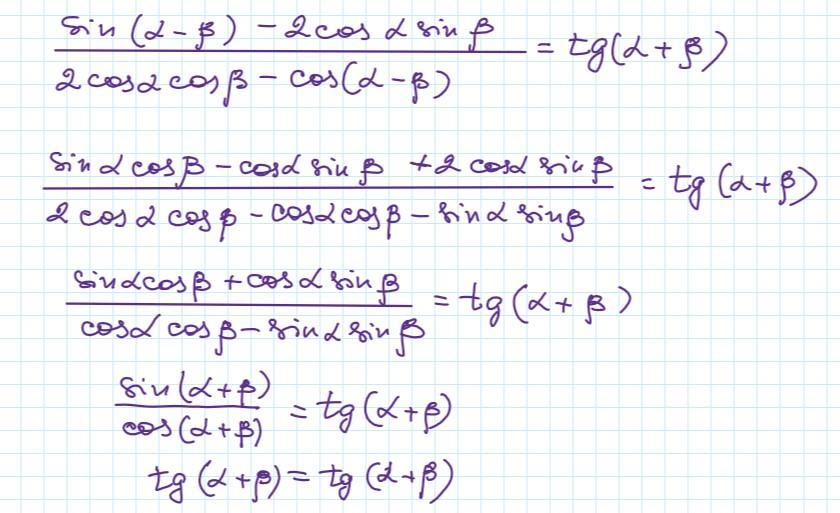
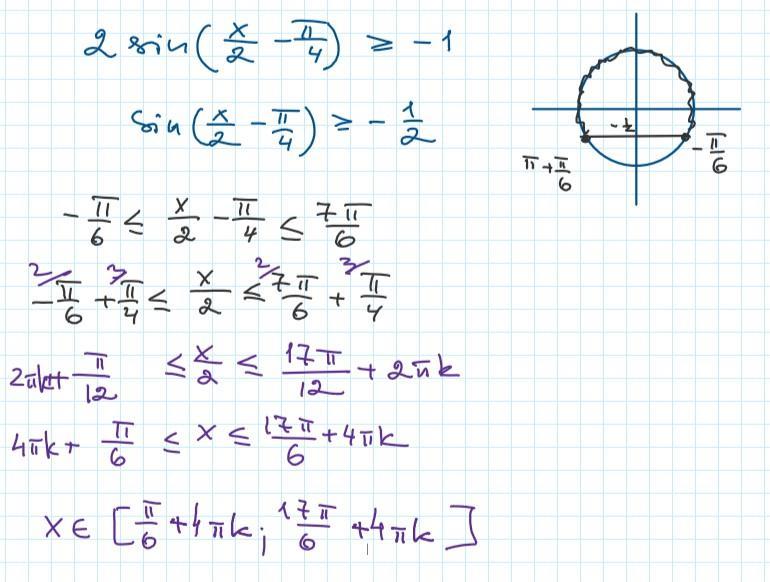
Ответил NNNLLL54

Ответ:

1) Доказать тождество . В условии описка. В числителе должна быть записана сумма, а не разность функций .

$\bf \displaystyle \frac{sin(\alpha -\beta )+2\, cos\alpha \, sin\beta }{2\, cos\alpha \, cos\beta -cos(\alpha -\beta )}=tg(\alpha +\beta )\\\\\\ \frac{sin(\alpha -\beta )+2\, cos\alpha \, sin\beta }{2\, cos\alpha \, cos\beta -cos(\alpha -\beta )}=\frac{(sin\alpha \, cos\beta -cos\alpha \, sin\beta )+2cos\alpha \, sin\beta }{2\, cos\alpha \, cos\beta -(cos\alpha \, cos\beta +sin\alpha \, sin\beta )}=$

$\displaystyle \bf =\frac{sin\alpha \, cos\beta +cos\alpha \, sin\beta }{cos\alpha \, cos\beta -sin\alpha \, sin\beta }=\frac{sin(\alpha +\beta )}{cos(\alpha +\beta )}=tg(\alpha +\beta )\\\\\\tg(\alpha +\beta )=tg(\alpha +\beta )$

2) Решить неравенство .

$\bf 2sin\Big(\dfrac{x}{2}-\dfrac{\pi }{4}\Big)\geq -1\ \ \ \to \ \ \ sin\Big(\dfrac{x}{2}-\dfrac{\pi }{4}\Big)\geq \dfrac{1}{2} \\\\\\-\dfrac{\pi }{6}+2\pi n\leq \dfrac{x}{2}-\dfrac{\pi }{4}\leq \dfrac{7\pi }{6}+2\pi n\ \ ,\ \ n\in Z\\\\\\\dfrac{\pi }{12}+2\pi n\leq \dfrac{x}{2}\leq \dfrac{17\pi }{12}+2\pi n\ \ ,\ \ n\in Z\\\\\\\dfrac{\pi }{6}+4\pi n\leq x\leq \dfrac{17\pi }{6}+4\pi n\ \ ,\ \ n\in Z\\\\\\x\in \Big [\ \dfrac{\pi }{6}+4\pi n\ ;\ \dfrac{17\pi }{6}+4\pi n\ \Big]\ \ ,\ \ n\in Z$

3) Найти значение выражения .

$\bf ctg\alpha =\dfrac{1}{3}\ \ ,\ \ \dfrac{sin\alpha +cos\alpha }{sin\alpha -cos\alpha }=\dfrac{sin\alpha \, (1+ctg\alpha )}{sin\alpha \, (1-ctg\alpha )}=\dfrac{1+ctg\alpha }{1-ctg\alpha }=\dfrac{1+\dfrac{1}{3}}{1-\dfrac{1}{3}}=\\\\\\=\dfrac{3+1}{3-1}=\dfrac{4}{2}=2$

Приложения:

Предыдущий вопрос

Следующий вопрос

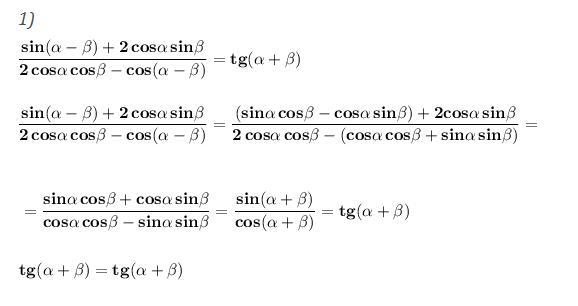
Новые вопросы

Математика, 8 месяцев назад

Фермер зібрав 30т зернових із них 12т кукурудзи.Скільки відсотків становить маса зібраної кукурудзи від маси зернових...

Химия, 8 месяцев назад

6. Айнур приготовила смесь из 3 г мела и 2 г сахара, добавила 50 мл воды и размешала смесь. Затем она отфильтровала смесь и получила белое твердое вещество на фильтровальной бумаге. Она высушила этот...

Алгебра, 11 месяцев назад

Подскажите пожалуйста...

Литература, 11 месяцев назад

Яка проблема не розкривається автором у новелі "Перевтілення"? проблема відчуження та знецінення особистості проблема самовідданості проблема митця і мистецтва проблема сімейних відносин...

Кыргыз тили, 6 лет назад

онол . зі - — 1- й -тапсырма. «Әр елдің салты басқа...». Бұйрықты сөйлемдер мен демеулік шылауларды, этикеттік сөз орамдарын пай- даланып, парталас көршіңмен Шығыс халықтарында жаңа жыл мейрамында...

Математика, 6 лет назад

СРОЧНО ПОМОГИТЕ!!! дам 20 баллов номер 3 а) б)...