допоможіть будь ласка, дуже потрібно.
Приложения:

Ответы на вопрос
Ответил dnepr1
0
Если дан угол, противоположный третьей стороне, то это и есть угол γ = С между двумя заданными сторонами.
Третья сторона находится по теореме косинусов,
c = √(a² + b² - 2ab*cosγ) = = √(8² + 6² - 2*8*6*cos 140°) ≈
≈ √(64 + 36 – 96*(-0,766044443)) ≈ √(100 + 73,54026654) ≈
≈ √173,54026654 ≈ 13,17346828.
Угол А находим по теореме синусов.
sin A /a = sin C/с.
sin A = sin A*c/a = sin 140°*13,17346828/8 = 0,3903528.
Угол А = arcsin0,3903528 = 22,976456°.
Угол В = 180 – 140 - 22,97645 = 17,023544°.
Ответил NNNLLL54
0
Ответ:
Применяем теорему косинусов :
Применим теорему синусов .
Приложения:
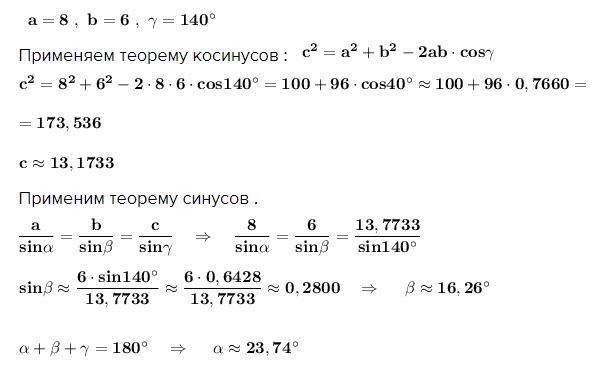
Новые вопросы
Химия,
11 месяцев назад
Математика,
11 месяцев назад
Английский язык,
11 месяцев назад
Қазақ тiлi,
11 месяцев назад