Допоможіть будь-ласка, дам 40 балів
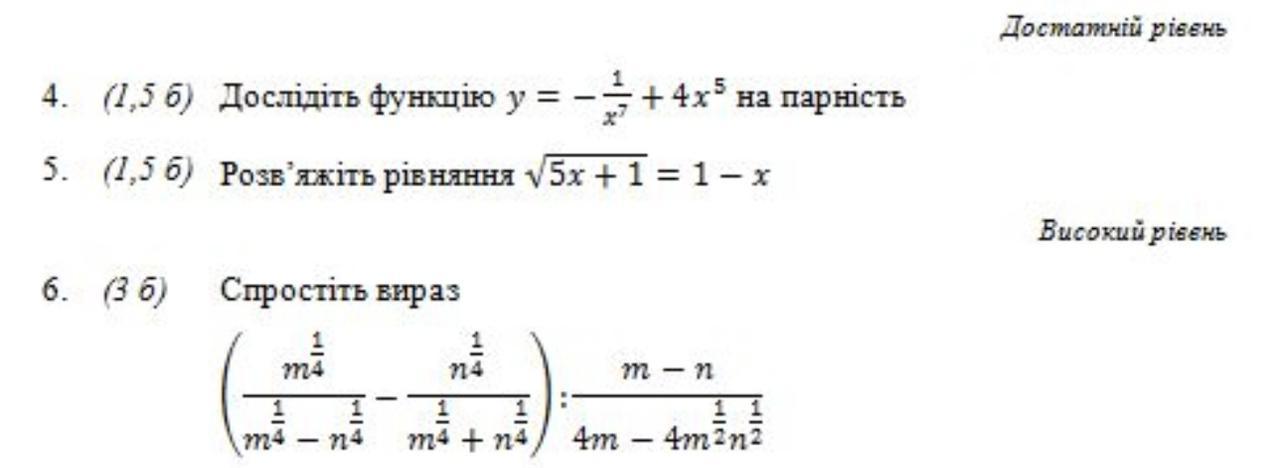
Ответы на вопрос
Відповідь:
Пояснення:
4 . Функція у = - 1/х⁷ + 4х⁵ - непарна , бо
у(- х ) = - 1/(- х )⁷ + 4(- х )⁵ = 1/х⁷ - 4х⁵ = - (- 1/х⁷ + 4х⁵ ) = - у( х ) для
всіх хЄ D( y ) ( D( y ) = R , крім х = 0 ) .
5 . √( 5x + 1 ) = 1 - x ;
[ √( 5x + 1 ) ]² = ( 1 - x )²; Перевірка .
5x + 1 = 1 - 2x + x² ; х = 0 ; √( 5*0 + 1 ) = 1 - 0 ;- правильно ;
x² - 7x = 0 ; х = 7 ; √( 5*7 + 1 ) = 1 - 7 ; - неправильно .
x( x - 7 ) = 0 ;
x₁ = 0 ; або х₂ = 7 . В - дь : х = 0 .
6 . [ Умову не переписую ] . Виконаємо зазначені дії :
1) m^(1/4)/[ m^(1/4) - n^(1/4) ] - n^(1/4)/[ m^(1/4) + n^(1/4) ] =
= [ m^(1/4)( m^(1/4)+n^(1/4) ) - n^(1/4)( m^(1/4) - n^(1/4) ) ]/[m^(1/2) - n^(1/2) ] =
= ( m^(1/2) + m^(1/4)n^(1/4) - m^(1/4)n^(1/4) + n^(1/2 ) )/[m^(1/2) - n^(1/2) ] =
= ( m^(1/2) + n^(1/2) )/( m^(1/2) - n^(1/2) ) ;
2) ( m^(1/2) + n^(1/2) )/( m^(1/2) - n^(1/2) ) : ( m - n )/( 4m - 4m^(1/2) n^(1/2)) =
= ( m^(1/2) + n^(1/2) )/( m^(1/2) - n^(1/2) ) * (4m - 4m^(1/2) n^(1/2))/( m - n ) =
= ( m^(1/2) + n^(1/2) )/( m^(1/2) - n^(1/2) ) * (4m^(1/2 )( m^(1/2) - n^(1/2) )/( m -
- n ) = 4m^(1/2)/( m^(1/2) - n^(1/2) ) .