Домашнє завдання
1) Знайдіть кути ромба, якщо його сторона утворює з діагоналями кути, один з яких учетверо менший від іншого.
2) Знайдіть кути ромба, якщо його висота дорівнює 9 см, а периметр – 72 см.
Ответы на вопрос
Ответил ludmilaksenija2005
0
Объяснение:
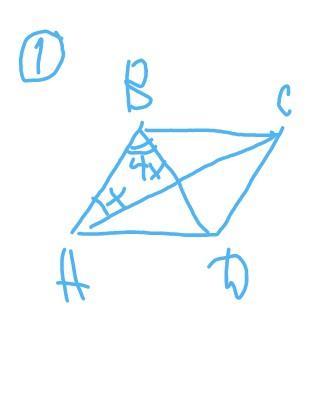
1.
АВСD - ромб
∠ВАС=х° ; ∠АВD=4x°
Диагонали ромба являются биссектрисами его углов, значит
∠ВАD=2∠BAC=2•x°
∠АВС=2∠АВD=2•4x=8x°
Сумма углов, прилежащих к одной стороне равна 180°:
∠ВАD+∠ABC=180
2x+8x=180
10x=180
x=18
∠BAD=2•10=20°
∠АВС=8•20=160°
В ромбе противолежащие углы равны:
∠ВСD=∠BAD=20°
∠АDC=∠ABC=160°
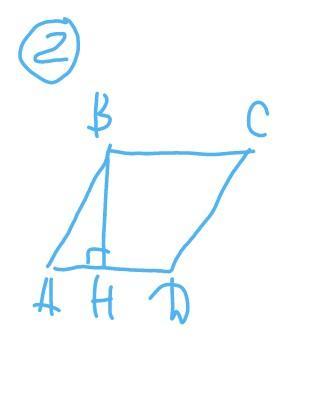
2.
АВСD -ромб
высота ВН=9 см
периметр Р=72 см
АВ=Р/4=72/4=18 см
∆АВН - прямоугольный:
sinA=BH/AB=9/18=1/2
∠A=30°
Сумма углов, прилежащих к одной стороне равна 180°
∠В=180-30=150°
в ромбе противолежащие углы равны:
∠С=∠А=30°
∠D=∠B=150°
Приложения:
Новые вопросы
Химия,
11 месяцев назад
Литература,
11 месяцев назад
Математика,
1 год назад
Английский язык,
6 лет назад