Докажите неравенство:
a) 12x ≤ (x + 3)^2;
б) x +4x + 5 > 0.
2. Известно, что 5 < х < 6 и 10 < у < 11. Оцените значение выражения:
a) 3x + 1y;
б) -2ху;
в) 2х - 0,2у; г) у/х
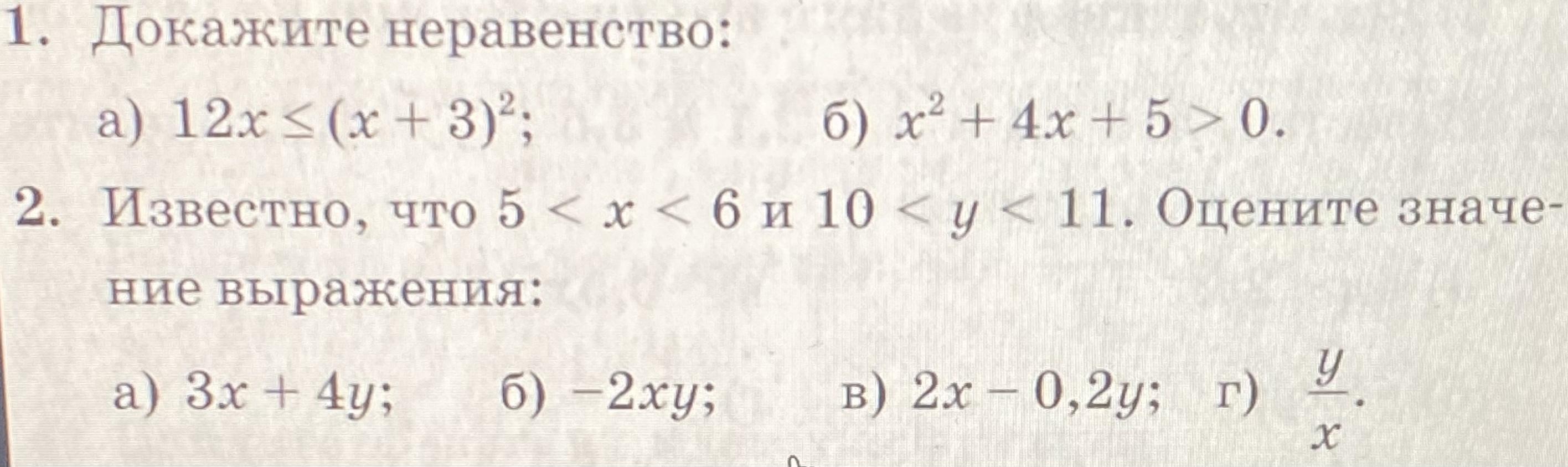
Ответы на вопрос
Ответ:
1. Неравенства доказаны.
2. а) 55 < 3x + 4y < 62; б) -132 < -2xy < -100; в) 7,8 < 2x - 0,2y < 10;
г) 5/3 < y/x < 11/5
Объяснение:
1. Докажите неравенство:
а) 12х ≤ (x + 3)²
- Квадрат суммы двух чисел:
(a + b)² = a² + 2ab + b²
12x ≤ x² + 6x + 9
0 ≤ x² + 6x + 9 - 12x
x² - 6x + 9 ≥ 0
- Квадрат разности двух чисел:
(a - b)² = a² - 2ab + b²
(х - 3)² ≥ 0
- Квадрат любого числа неотрицателен.
Доказано.
б) х² + 4х + 5 > 0
Выделим полный квадрат:
(х² + 4x + 4) + 1 > 0
(x + 2)² + 1 > 0
(x + 2)² ≥ 0 ⇒ (x + 2)² + 1 > 0
Доказано.
2. Известно, что 5 < x < 6 и 10 < y < 11. Оцените значения выражений:
а) 3х + 4у
- Если обе части неравенства умножить или разделить на положительное число, то получим неравенство равносильное данному.
5 < x < 6 | · 3
15 < 3x < 18
10 < y < 11 | · 4
40 < 4y < 44
- Неравенства одного знака можно сложить почленно:
₊ 15 < 3x < 18
40 < 4y < 44
-----------------------
55 < 3x + 4y < 62
б) -2ху
- Неравенства одного знака можно умножать почленно:
ₓ 5 < x < 6
10 < y < 11
--------------------
50 < xy < 66
- Если обе части неравенства умножить на отрицательное число, то знак неравенства перевернется.
50 < xy < 66 | · (-2)
-100 > -2xy > -132
или
-132 < -2xy < -100
в) 2х - 0,2у
5 < x < 6 | · 2
10 < 2x < 12
10 < y < 11 | · (-0,2)
-2 > -0,2y > -2,2
или
-2,2 < -0,2y < -2
Сложим полученные неравенства:
₊ 10 < 2x < 12
-2,2 < -0,2y < -2
------------------------------
7,8 < 2x - 0,2y < 10
г) y/x
- Свойство неравенств:
Если a > b > 0, то 1/а < 1/b
5 < x < 6
1/5 > 1/x > 1/6
или
1/6 < 1/x < 1/5
Умножим неравенства:
ₓ 1/6 < 1/x < 1/5
10 < y < 11
------------------------
10/6 < y/x < 11/5
сократим:
5/3 < y/x < 11/5