Докажите неравенство
Приложения:
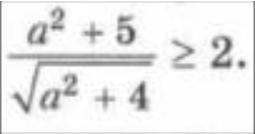
Ответы на вопрос
Ответил bb573878
2
Ответ:
Объяснение:
неравенство верно, в числителе квадрат числа, ≥0
знаменатель >0
makviv75:
МНЕ ПОМОГИТЕ ПОЖАЛУЙСТА УМОЛЯЮ
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Английский язык,
6 лет назад
Алгебра,
6 лет назад