Алгебра, вопрос задал ЛисичкаАлисочка , 9 лет назад

Докажите, что значение выражения не зависит от n

Приложения:

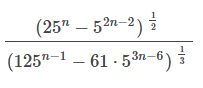
Ответы на вопрос

Ответил Эксперт5

$frac{(25^{n}-5^{2n-2})^{ frac{1}{2}} }{(125^{n-1}-61*5^{3n-6})^{ frac{1}{3} }}= frac{(5^{2n}-5^{2n-2})^{ frac{1}{2} }}{(5^{3n-3}-61*5^{3n-6})^{ frac{1}{3} }}= frac{ sqrt{5^{2n}(1-5^{-2})} }{ sqrt[3]{5^{3n-3}(1-61*5^{-3})} }=\\= frac{5^n(1- frac{1}{25}) }{5^{n-1}(1- frac{61}{125}) }= frac{5^nsqrt{ frac{25-1}{25}} }{5^{n-1} sqrt[3]{ frac{125-61}{125} } }= frac{5^{n-n+1}sqrt{ frac{24}{25}} }{sqrt[3]{ frac{64}{125} } } =\\= frac{5* frac{ 2sqrt{6} }{5} }{ frac{4}{5} }=$
=2,5√6

В ответе не содержится переменная n, следовательно, значение выражения не зависит от n

Ответил ЛисичкаАлисочка

Огромное спасибо)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська література, 2 года назад

помогите с тестом по украинскому,пожалуйста(Даю 30 баллов)...

Литература, 2 года назад

ПОМОГИТЕ ПРОШУ УМОЛЯЮ!!!!!!ЭТО ФОРМАТИВНАЯ РАБОТА ПРОШУ ПРОШУ ПРОШУ...

Алгебра, 9 лет назад

Выполните действие : ( а+2 корень квадратный с ) ( а-2 корень квадратный с) ( корень квадратный 3 - корень квадратный 6 ) во 2 степени Пожалуйста очень срочно)))) в 1 примере под корнем С...

Геометрия, 9 лет назад

один из внешних углов треугольника равен 24 градусам. Углы, не смежные с данным внешним углом, относятся как 1:2. Найдите наибольший из них...

Физика, 9 лет назад

помогиете поф физике 12-13-14 задачи не могу понять их:(...

Физика, 9 лет назад

При напряжении 2 кВ сопротивление проводника равно 200 Ом. Какова сила тока в проводнике?