Докажите,что прямые параллейны.
Ответы на вопрос
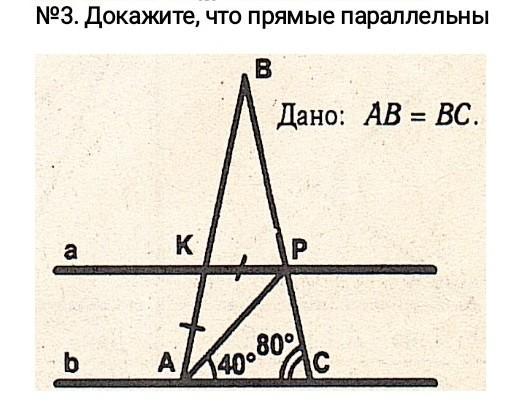
Ответ:Если по условию задачи АВ=ВС,то треугольник АВС равнобедренный,а значит,что углы при основании равны между собой
<ВАС=<С=80 градусов
Тогда
<КАР=80-40=40 градусов
Треугольник АКР равнобедренный по условию задачи,значит
<КАР=<АРК=40 градусов
<АКР=180-40•2=100 градусов
Треугольник АРС
<АРС=180-(40+80)=60 градусов
<КРС=40+60=100 градусов
Четырёхугольник АКРС на самом деле равнобокая трапеция,т к углы при каждом основании равны между собой
Мы можем утверждать,что прямые параллельны хотя бы потому,что по определению основания трапеции параллельны,т е
КР || АС
Но ещё и равны накрест лежащие углы
<РАС=<АРК=40 градусов,как накрест лежащие при КР || АС и секущей АР
Объяснение:
Ответ:
<ВАС=<ВСА=80 градусов, т. к АВ=ВС, тр-к АВС-равнобедренный
<КАС=<РСА=<ВАС=80 градусов,
<КАР=<АРК=<КАС-<РАС=80-40=40 градусов,
<АКР=180-2×<КАР=180-2×40=100 градусов,т.к
тр-к АКР - равнобедренный (АК=КР)
Сумма односторонних углов равна 180 градусов :
<АКР+<КАС=100+80=180 градусов,
значит прямые а и b параллельны