Докажите,что биссектриса внешнего угла при вершине равнобедренного треугольника,противолежащей основанию,параллельна основанию

Внешний угол при вершине треугольника равен сумме внутренних углов треугольника, не смежных с ним.

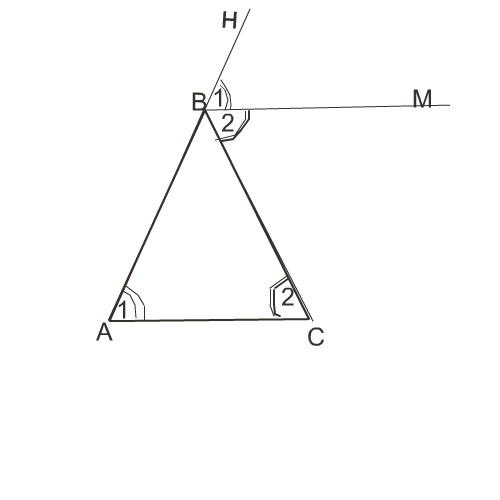
Рассмотрим треугольник АВС.

Угол СВН - внешний угол при вершине, противоположной основанию.

ВМ- биссектриса этого угла. Она делит угол на два равных угла 1 и 2.

Так как внешний угол при В равен сумме внутренних углов А и С, а треугольник АВС равнобедренный и углы при его основании равны между собой, все выделенные углы также равны между собой.

Углы под номером 1 -равные соответственные при прямых АС и ВМ
и секущей АВ
Углы под  номером 2 - равные накрестлежащие при прямых АС и ВМ
и секущей ВС
Если при пересечении двух прямых третьей внутренние накрестлежащие углы равны, то прямые параллельны.