Алгебра, вопрос задал nurislam2016a , 6 лет назад

Докажи что значение выражения не зависит от синуса и косинуса

Приложения:

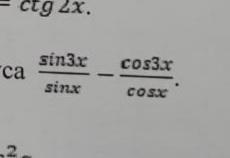
Ответы на вопрос

Ответил lilyatomach

Ответ:

$\dfrac{sin3x}{sinx} -\dfrac{cos3x}{cosx} =2$ и не зависит от синуса и косинуса

Объяснение:

Докажем, что выражение не зависит от синуса и косинуса

Для этого выполним вычитание дробей, приведя дроби к общему знаменателю

$\dfrac{sin3x}{sinx} -\dfrac{cos3x}{cosx} =\dfrac{sin3x\cdot cosx-cos3x\cdot sinx}{sinx\cdot cosx}$

Воспользуемся формулой $\sin(\alpha- \beta )= sin\alpha \cdot cos\beta -cos\alpha \cdot sin\beta$

и упростим числитель полученной дроби

$\dfrac{sin(3x-x)}{sinx\cdot cosx} =\dfrac{sin2x}{2sinx\cdot cosx}$

В числителе дроби получили синус двойного угла, применим формулу

$\sin2\alpha =2\sin\alpha \cdot \cos\alpha .$

Получим

$\dfrac{2sinx\cdot cosx}{sinx\cdot cosx} =2$

Тогда значение выражения не зависит от синуса и косинуса, так как получили в результате преобразований число 2.

Новые вопросы

История, 1 год назад

История, 1 год назад

История, 6 лет назад

Русский язык, 6 лет назад

История, 8 лет назад

Математика, 8 лет назад