Алгебра, вопрос задал berlizovakysa , 7 лет назад

Доказать Тождество (номер 3)

Приложения:

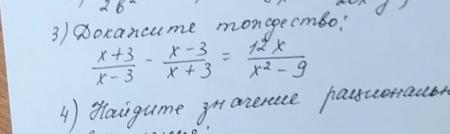
Ответы на вопрос

Ответил Universalka
0

frac{x+3}{x-3}-frac{x-3}{x+3}=frac{(x+3)*(x+3)-(x-3)*(x-3)}{(x-3)(x+3)}=frac{x^{2}+6x+9-x^{2}+6x-9}{(x-3)(x+3)}=frac{12x}{x^{2}-9}\\frac{12x}{x^{2}-9}=frac{12x}{x^{2}-9}

Тождество доказано

Ответил sangers1959
0

Ответ:

Объяснение:

frac{x+3}{x-3} -frac{x-3}{x+3} =frac{(x+3)^{2} -(x-3)^{2} }{(x+3)(x-3)} =frac{x^{2} +6x+9-(x^{2} -6x+9)}{x^{2} -9}=frac{x^{2} +6x+9-x^{2} +6x-9}{x^{2}-9 } =frac{12x}{x^{2}-9. }

Предыдущий вопрос
Следующий вопрос
Новые вопросы