Алгебра, вопрос задал dayana24sh , 6 лет назад

доказать неравенство за 97баллов​

Приложения:

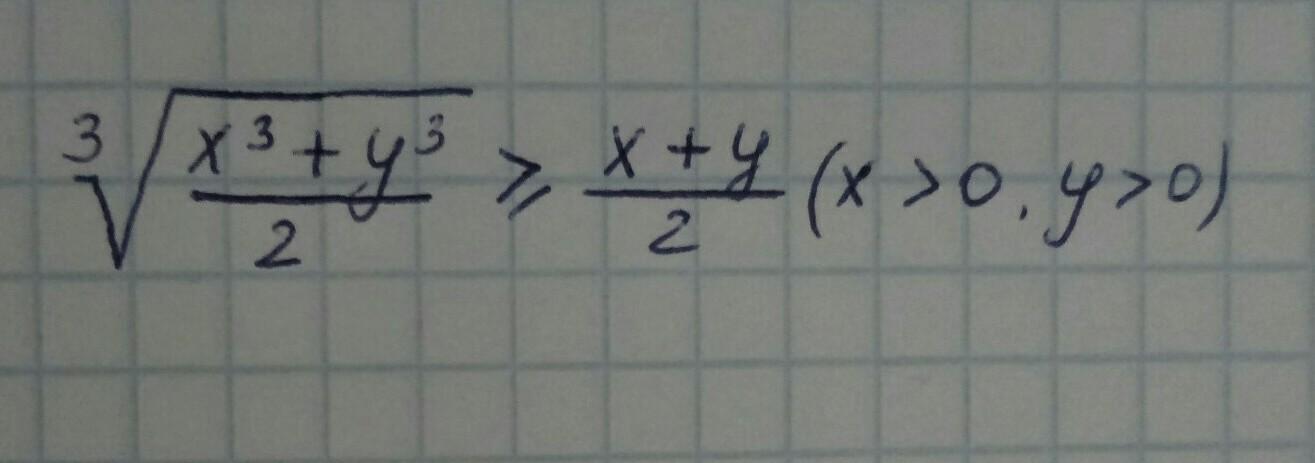
Ответы на вопрос

Ответил bb573878
1

Ответ:

Объяснение:

\displaystyle\sqrt[3]{\frac{x^3+y^3}{2} } \geq \frac{x+y}{2} ~~~~~~~(x>0,y>0)

обе части положительны, возведем в куб

\displaystyle\frac{x^3+y^3}{2} \geq \frac{(x+y)^3}{8} \\\\4(x^3+y^3)\geq (x+y)^3\\\\4(x+y)(x^2-xy+y^2)-(x+y)^3\geq 0\\\\(x+y)(4x^2-4xy+4y^2-x^2-2xy-y^2)\geq 0\\\\(x+y)(3x^2-6xy+3y^2)\geq 0\\\\3(x+y)(x^2-2xy+y^2)\geq 0\\\\3(x+y)(x-y)^2\geq 0

данное неравенство верно:

второй множитель х+у больше нуля,

поскольку х>0,y>0

(x-y)²≥0  квадрат любой величины ≥0

исходное неравенство тоже верно

доказано

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
Напишите как можно заменить слово "город" , а то у меня в сочинение слишком часто повторяется это слово...
Русский язык, 1 год назад
имена с двумя пппппппп...
Математика, 6 лет назад
2, 5|3x - 2| = 10 пжжжжжж 50 баллов СРОЧНО УМОЛЯЮ ​...
Русский язык, 6 лет назад
Пожалуйста ответьте дам 5 звёзд осталось на выполнение 2 часа Найдите слова правописание приставок в которых зависит от глухости/звонкости последующей согласной. Всплыть Накормить Подача...
Биология, 8 лет назад
Используя учебник, интернет-источник, энциклопедии, словари, справочники, научно-популярную литературу, составьте план и на его основе подготовьте презентацию"Значение моллюсков в природе и жизни...
Математика, 8 лет назад
Встоловую привезли 17кг моркови, а картофеля- на 43кг больше. Сколько всего килограммов овощей привезли в столовую? Напишите с краткой записью.