Алгебра, вопрос задал mrgoofy217 , 7 лет назад

Доказать что при всех допустимых значениях α справедливо равенство

Приложения:

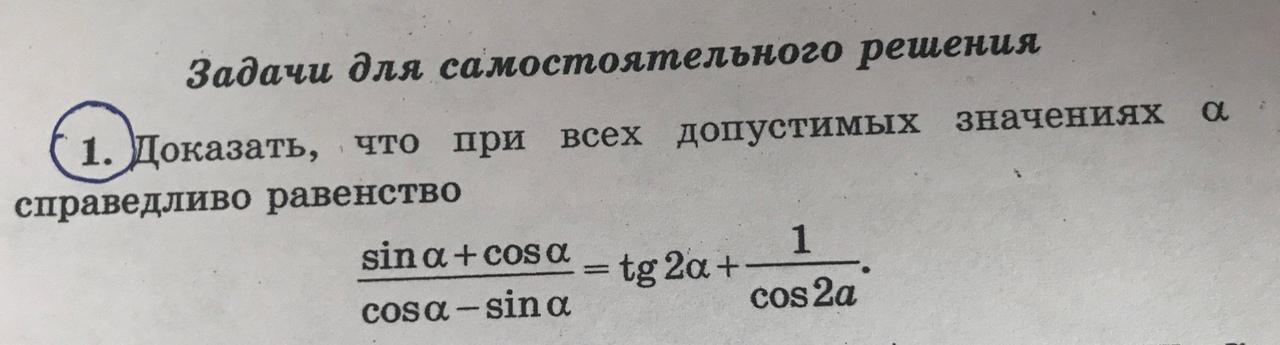
Ответы на вопрос

Ответил LordTutus

В левой части выражения (для простоты cosα = c, sinα = s):

$frac{s+c}{c-s} = frac{s+c}{c-s}*frac{c-s}{c-s} =frac{c^2-s^2}{(c-s)^2} = frac{2c^2-1}{1-2cs} =$

В последнем переходе использовалось основное тригонометрическое тождество: c² + s² = 1.

Переходим к двойному углу:

$=frac{ cos 2alpha}{1-sin 2alpha}$

Далее помножим числитель и знаменатель на cos2α:

$frac{cos^2 2alpha}{(1 - sin 2alpha)cos 2alpha} = frac{1 - sin^2 2alpha}{(1 - sin 2alpha)cos 2alpha} = frac{1 + sin 2alpha}{cos 2alpha} = frac{1}{cos 2alpha} + frac{ sin 2alpha}{cos 2alpha} = frac{1}{cos 2alpha} + tan 2alpha$

Получили искомое выражение.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

write the plurals child man,box,leaf,watch,boy,party помогите срочно...

Українська мова, 1 год назад

Написати 2-5 речень з фразеологізмами...

Математика, 7 лет назад

Найди значения выражений а-7 и а+8при а=23,а=60,а=57,а=92...

Математика, 7 лет назад

В мае кг картофеля стоил 200тг.В июне его цена снизилась на 30%.Какова разница в стоимости покупки 3кг картофеля в мае и июне?

Алгебра, 8 лет назад

Заполните таблицу. За такие ответы как: арнеолл533$анлга и т.д. БУДУ БАНИТЬ!

Математика, 8 лет назад

КАК РЕШИТЬ (Х+5/12)-9/20=11/15...