Алгебра, вопрос задал danmadro77 , 7 лет назад

Доказать, что при всех допустимых значениях a справедливо равенство.

Приложения:

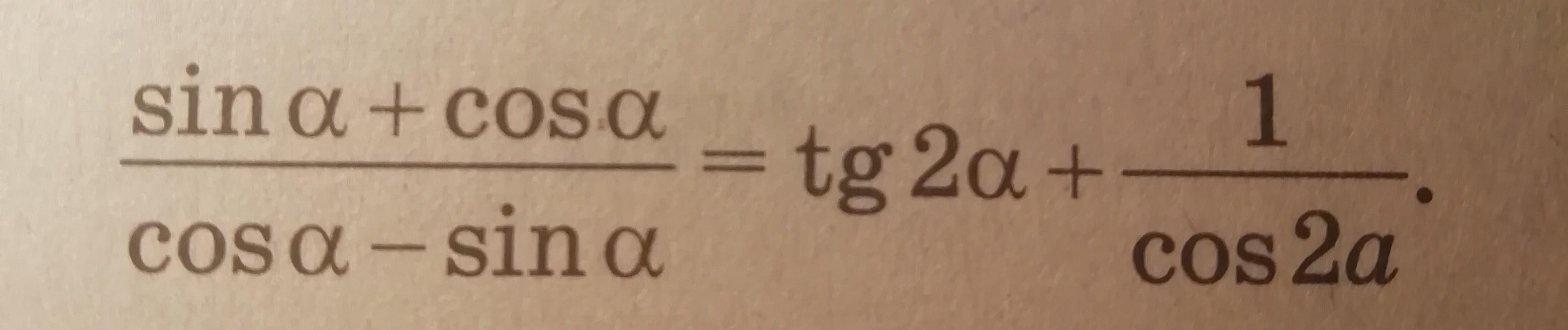
Ответы на вопрос

Ответил Correlation

Умножим числитель и знаменатель дроби на cosa + sina, получим:

$displaystyle frac{sin alpha+cosalpha}{cosalpha-sinalpha}=frac{(sinalpha+cosalpha)^2}{(cosalpha-sinalpha)(cosalpha+sinalpha)}=frac{1+sin2alpha}{cos2alpha}={rm tg}2alpha+frac{1}{cos2alpha}$

Ответил Universalka

Преобразуем правую часть тождества :

$tg2alpha+frac{1}{Cos2alpha}=frac{Sin2alpha}{Cos2alpha}+frac{1}{Cos2alpha}=frac{Sin2alpha+1 }{Cos2alpha}=frac{Cos^{2}alpha+2Sinalpha Cosalpha+Sin^{2}alpha}{Cos^{2}alpha-Sin^{2}alpha}=frac{(Cosalpha+Sinalpha)^{2}}{(Cosalpha+Sinalpha)(Cosalpha-Sinalpha)}=frac{Sinalpha+Cosalpha}{Cosalpha-Sinalpha}\\frac{Sinalpha+Cosalpha}{Cosalpha-Sinalpha}=frac{Sinalpha+Cosalpha}{Cosalpha-Sinalpha}$

Тождество доказано

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

сочинение на тему выходной день для 5 класса...

Английский язык, 1 год назад

5 класс. ---- Complete the text. Use: from, fiends, letter, longest, the country, summer, like. ---- Hi Steve, Thank you for your letter. It was nice to hear_______you. You know,the summer holidays...

Алгебра, 7 лет назад

Найдите разность между наибольшим и наименьшим значениями функции y=x^2 на отрезке [ -1;3 ] ( см. рис. 17 ).

Математика, 7 лет назад

На сколько сумма всех чётных чисел пяти первых сотен больше суммы всех нечётных чисел пяти первых сотен?

История, 8 лет назад

200-летний период в истории Русской Православной Церкви, закончившийся восстановлением патриаршества на Поместном Соборе 1917–1918 годов, принято называть... ПОМОГИТЕ ПОЖАЛУЙСТА ОТВЕТИТЬ НА ВОПРОС...

Геометрия, 8 лет назад

Помогите ПОЖАЛУЙСТА!!! Очень срочно!!! Один из смежных углов меньше другого на 120 градусов. Найдите величину меньшего угла.