Алгебра, вопрос задал Fazzika , 7 лет назад

Доказать, что ... для любых действительных x и y, имеющих одинаковые знаки

Приложения:

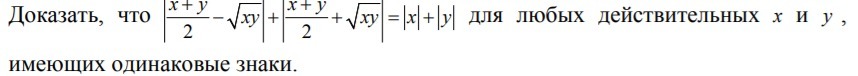
Ответы на вопрос

Ответил 7x8

$|x|+|y|= begin{cases} x+y x,y>0\ -x-y x,y<0end{cases}$

--------------------------

1) для $x,y>0$

$left|frac{x+y}{2}-sqrt{xy}}right| +left|frac{x+y}{2}+sqrt{xy}} right| =$

$frac{1}{2} left|x+y-2sqrt{xy}}right| + frac{1}{2} left|x+y+2sqrt{xy}} right| =$

$frac{1}{2} left|( sqrt{x}- sqrt{y} )^2 right| + frac{1}{2}left| ( sqrt{x}+ sqrt{y} )^2right| =$

$frac{1}{2} ( sqrt{x}- sqrt{y} )^2 + frac{1}{2}( sqrt{x}+ sqrt{y} )^2 =$

$frac{1}{2} (x-2 sqrt{xy}+y ) + frac{1}{2}( x+2sqrt{xy}+ y )=x+y$

--------------------------

2) для $x,y<0$

$left|frac{x+y}{2}-sqrt{xy}}right| +left|frac{x+y}{2}+sqrt{xy}} right| =$

$frac{1}{2} left|x+y-2sqrt{xy}}right| + frac{1}{2} left|x+y+2sqrt{xy}} right| =$

$frac{1}{2} left|( sqrt{-x}- sqrt{-y} )^2 right| + frac{1}{2}left| ( sqrt{-x}+ sqrt{-y} )^2right| =$

$frac{1}{2} ( sqrt{-x}- sqrt{-y} )^2 + frac{1}{2}( sqrt{-x}+ sqrt{-y} )^2 =$

$frac{1}{2} (-x-2 sqrt{xy}-y ) + frac{1}{2}( -x+2sqrt{xy}- y )=-x-y$

--------------------------

$left|frac{x+y}{2}-sqrt{xy}}right| +left|frac{x+y}{2}+sqrt{xy}} right| =|x|+|y|$

для любых действительных x и y, имеющих одинаковые знаки

Новые вопросы

Физика, 1 год назад

Геометрия, 1 год назад

Физика, 7 лет назад

Математика, 7 лет назад

Математика, 8 лет назад

Математика, 8 лет назад