Доказать, что для любого натурального n 
igorShap:
К слову, если поделить обе части на (n!)^2, слева получится количество бинарных векторов длины 2n, у которых по n штук 1 и 0, а справа - общее количество бинарных векторов длины 2n, откуда и следует верность неравенства
Ответы на вопрос
Ответил amanda2sempl
2
Пошаговое объяснение: на снимках
Приложения:

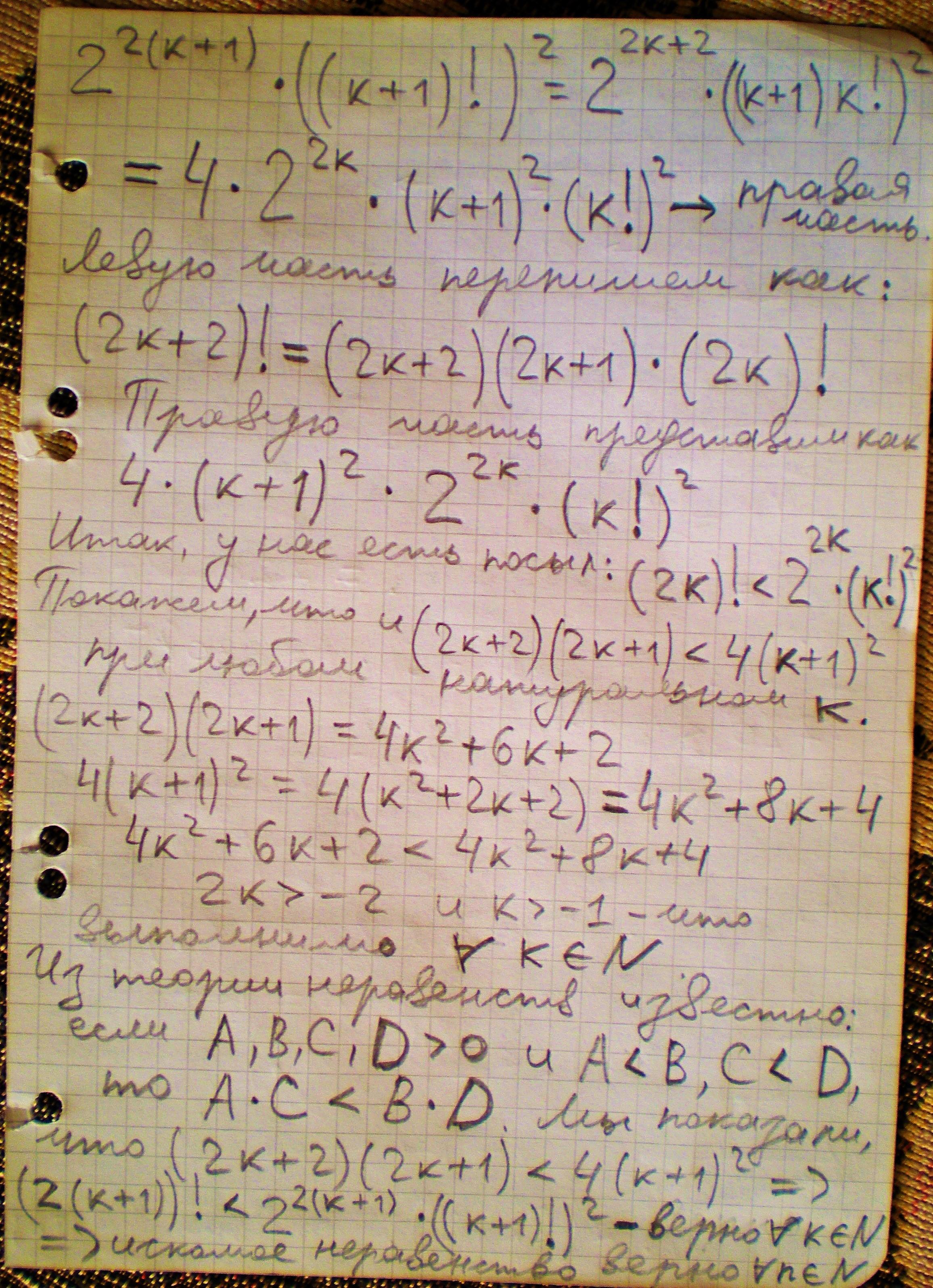
Новые вопросы