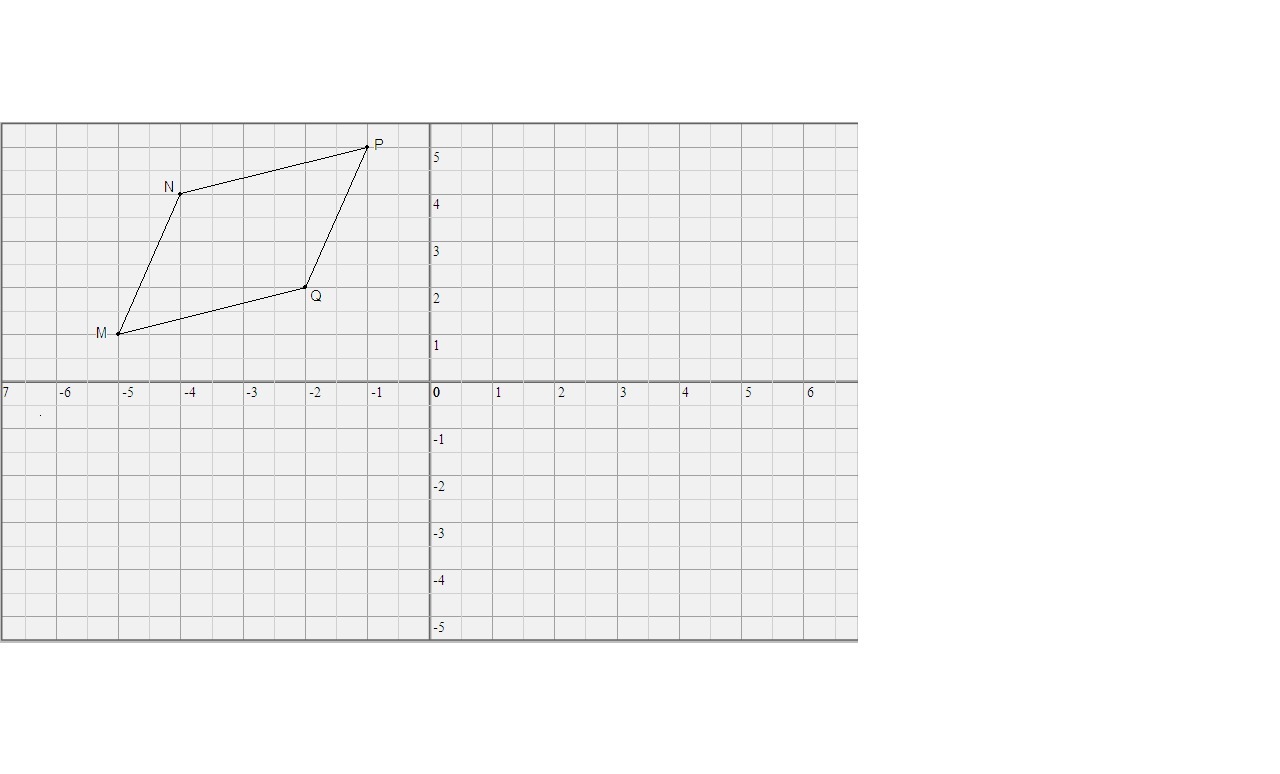
Доказать, что четырёхугольник MNPQ - параллелограмм, если M(-5;1), N(-4;4), P(-1;5); Q(-2;2). 

=> MQ не параллельно PN => MNPQ - не является параллелограммом! (((

M(- 5 ; 1),  N(- 4 ; 4), P(- 1 ; 5), Q(- 2 ; 2)

↑MN = (- 4  - ( - 5) ; 4 - 1) = (1 ; 3)
↑QP = (- 1 - (-2) ; 5 - 2) = (1 ; 3)

Векторы MN и QP равны, значит противоположные стороны четырехугольника MNPQ равны и параллельны, а значит это параллелограмм.

Стороны параллелограмма не параллельны осям координат, поэтому соответствующие координаты не равны.