добрый вечер,даю 100 баллов за подробную постройку графика с соблюдением алгоритма.
Алгоритм:
1. Область определения.
2. Четность и нечетность функции.
3. Периодичность.
4. Нули функции, промежутки анакопостоянства.
5. Точка разрыва и поведение функции вблизи точек разрыва.
6. Асимптомы.
7. Промежутки возрастания и убывания.
8. Исследования на выпуклость. Составление таблицы.
9. Составление таблицы некоторых значений функции.
10. По результатам исследования строим график.
Прошу помочь, так как от этого графика зависит моя жизнь.
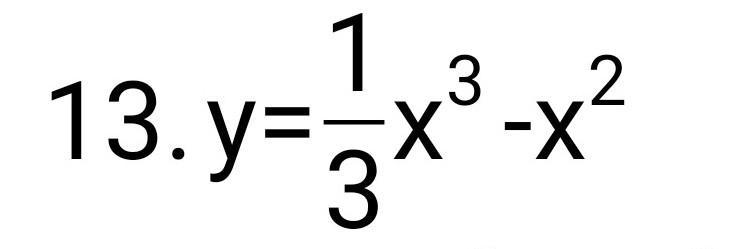
Ответы на вопрос
Ответ:
Пошаговое объяснение:
1) ООФ вся числовая ось
2) четность
f(-x) = f(x)
(1/3)(-x)³ - (-x)² ≠ (1/3)(x)³ - (x)² - функция не является четной
f(-x)=-f(x)
(1/3)(-x)³ - (-x)² ≠-( (1/3)(x)³ - (x)²) - функция не является нечетной
3) функция не периодична
4. Нули функции, промежутки знакопостоянства
(1/3)x²(x-3) = 0; x₁ = 0; x₂ = 3 -это нули функции
знакопостоянство
(-∞; 0) f(-1)= -1/3 -1 < 0
(0; 3) f(1)= 1/3 - 1 < 0
(3; +∞) f(4) (1/3)*4³ - 4²= 21,(3) - 16 > 0
5. Точка разрыва и поведение функции вблизи точек разрыва.
точек разрыва функция не имеет на всей ООФ
6. Асимптоты
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
находим k
поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.
7. Промежутки возрастания и убывания.
f'(x) = x²-2x
х(х-2)=0; x₁ = 0, x₂ = 2 это критические точки
(-∞; 0) f'(x) > 0 - функция возрастает
(0; 2) f'(x) < 0 - функция убывает
(2; +∞) f'(x) > 0 - функция возрастает
8. Исследования на выпуклость
вторая производная.
f''(x) = 2x-2
2x-2 = 0; 2(x-1) = 0 x₁ = 1 - это точка перегиба
(-∞; 1) f''(x) < 0 - функция выпукла
(1; +∞) f''(x) > 0 - функция вогнута
9. Составление таблицы некоторых значений функции.
x -1 0 1 2
y -4/3 0 -2/3 -4/3
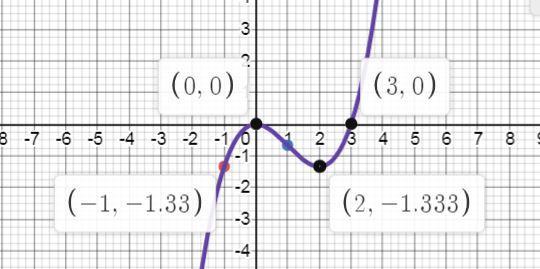
10 график на рисунке