длина стороны ромба равна 10 см, а диагонали относятся как 3:4. Площадь ромба равна: а) 48см² б) 24см² в) 12 см² г) 96см²
Ответы на вопрос
Ответил Аноним
0
Ответ:
96см²
Объяснение:
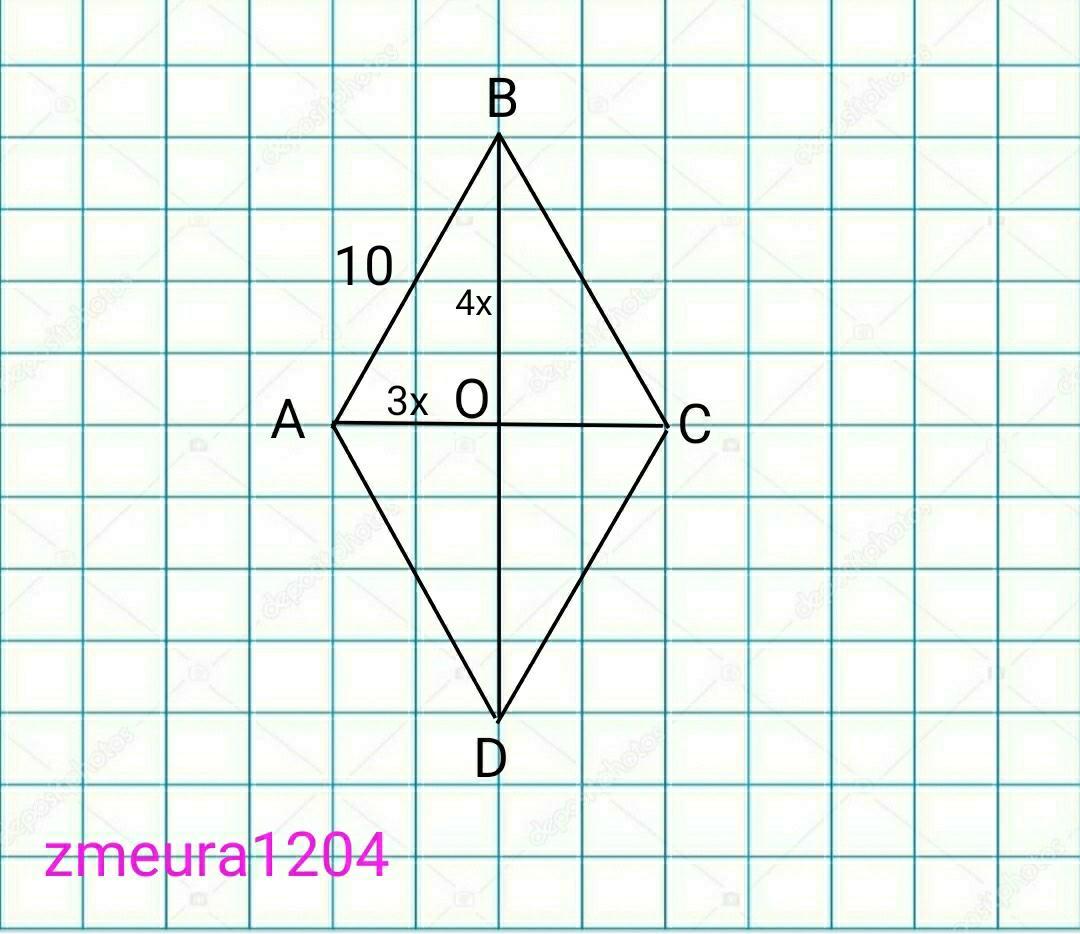
Диагонали относятся 3:4 АС:BD, то и их половины также AO:BO=3:4.
Пусть АО будет 3х; ВО будет 4х.
По теореме Пифагора
АВ²=АО²+ВО²
Составляем уравнение
(3х)²+(4х)²=10²
25х²=100
х=√4
х=2
АО=2*3=6см
ВО=2*4=8см
АС=2*АО=2*6=12см
ВD=2*BO=2*8=16см
S=AC*BD/2=12*16/2=96см²
Приложения:
Ответил Пеппер
0
Ответ:
96 см²
Объяснение:
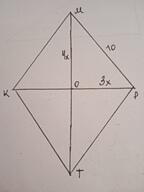
Дано: КМРТ - ромб МР=10 см, МО:РО=4:3. S - ?
Площадь ромба равна половине произведения диагоналей.
Пусть МО=4х см, РО=3х см, тогда по теореме Пифагора
МР²=МО²+РО²
100=16х²+9х²; 100=25х²; х²=4; х=2.
МО=ТО=4*2=8 см; МТ=16 см
РО=КО=3*2=6 см.; КР=12 см
S=1/2 * 16 * 12 = 96 cм²
Приложения:
Аноним:
Неправильно.
Новые вопросы