Математика, вопрос задал korulenkoroman59 , 2 года назад

Дифференциальные уравнения 2 порядка

Приложения:

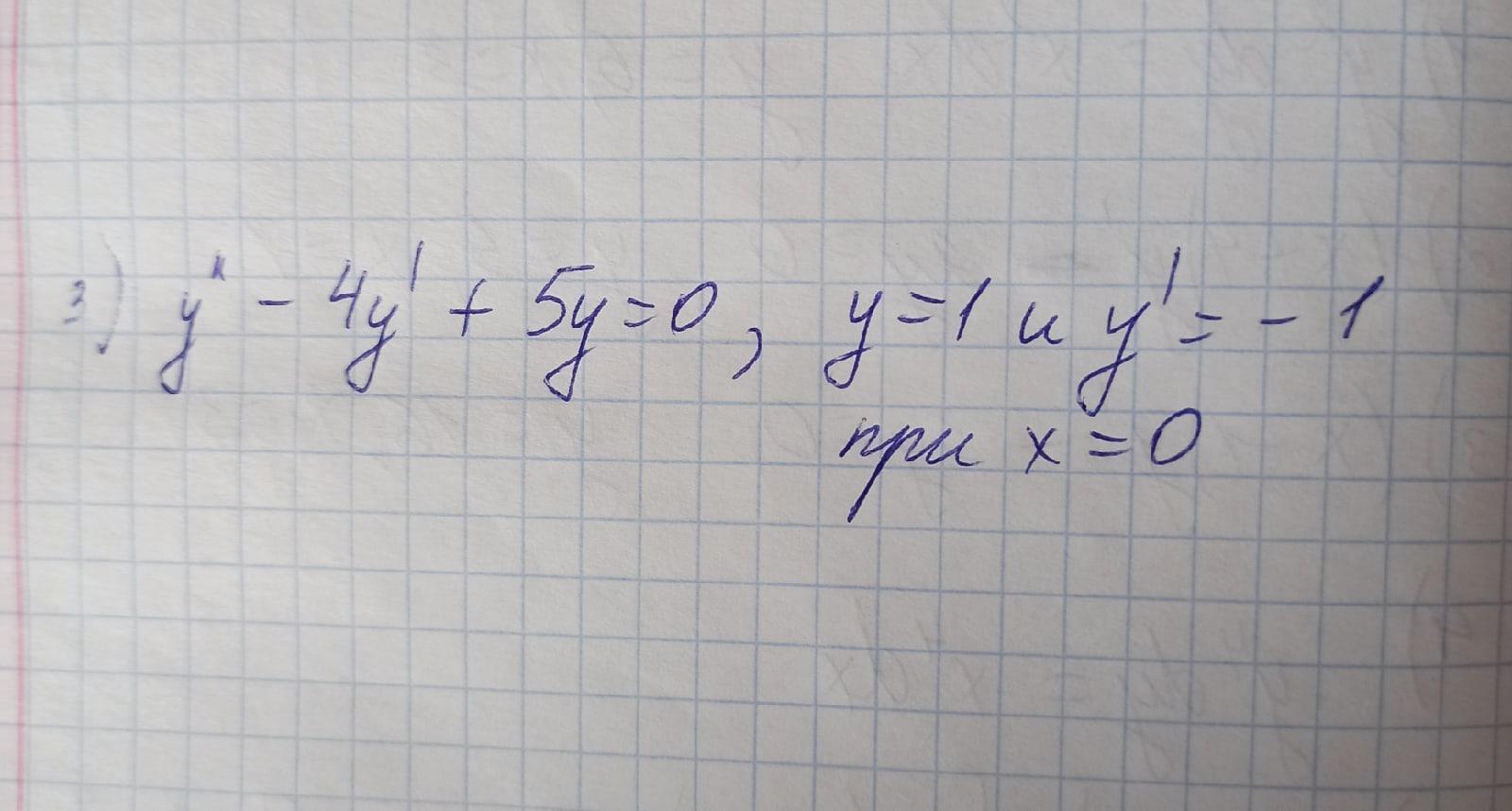
Ответы на вопрос

Ответил Miroslava227

Ответ:

$y'' - 4y' + 5y = 0$

Замена:

$y = {e}^{kx} \\ {e}^{kx} ( {k}^{2} - 4k + 5) = 0 \\ D = 16 - 20 = - 4 \\ k1 = \frac{4 + \sqrt{ - 4} }{2} = \frac{4 + 2i}{2} = 2 + i \\ k2 = 2 - i$

$y = {e}^{2x} (C1 \sin(x) + C2 \cos(x))$

общее решение.

$y( 0) = 1 \\ y'(0) = - 1$

$y' = 2 {e}^{2x} (C1 \sin(x) + C2 \cos(x) ) + {e}^{2x} (C1 \cos(x) - C2 \sin(x) )$

В систему:

$1 = {e}^{0} (C1 \sin(0) + C2 \cos(0) ) \\ - 1 = 2 {e}^{0} (C1 \sin(0) + C2\cos(0) ) + {e}^{0} (C1 \cos(0) ) - C2 \sin(0) ) \\ \\ C2 = 1 \\ 2C2 + C1 = - 1 \\ \\C2 = 1 \\ C1 = - 1 - 2C2 = - 1 - 2 = - 3$

$y = {e}^{2x} ( - 3 \sin(x) + \cos(x))$

Частное решение

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

помогите пожалуйста ) номер 10 б ) заранее спасибо )...

Русский язык, 1 год назад

сочинение 5 класс письмо об одном из удачно проведенных вечеров или дней...

Алгебра, 2 года назад

СРОЧНО!!!! В арифметической прогрессии (аn), а1 = - 111, d = 3. Укажи наименьшее число членов этой прогрессии, сумма которых будет положительной. 77 75 76 74...

Математика, 2 года назад

Теплоход Кулибин идет по реке Лена со скоростью 55 км/ч. Впереди теплохода идет баржа со скоростью 25 км/ч. Какое расстояние будет между ними через 3 ч, если сейчас баржа впереди теплохода на 50 км?

География, 7 лет назад

какие природные условия необходимые для разведения овец есть в Великобритании?

Математика, 7 лет назад

Реши задачу Вычисли и запиши ответ в вазе лежит 25 одинаковых конфет Какое самое большое число конфет маша может взять из вазы для того чтобы поровну угостить ими семерых Одноклассников которые к ним...