Дифференциальное исчисление-Полное исследование функции
y=x^3-6x^2+9x+1,[0;4]
1. Найти область определения функции.
2. Установить чётность (нечётность) и периодичность функции.
3. Исследовать поведение функции на границах области определения и найти асимптоты графика функции.
4. Найти интервалы монотонности и экстремумы функции.
5. Найти интервалы направления выпуклости и точки перегиба графика функции.
6. Найти точки пересечения с осями координат и дополнительные точки; построить график функции.
Ответы на вопрос
Ответил xxxeol
0
ДАНО
х³-6х²+9х+1 на интервале Х∈[0,4].
ИССЛЕДОВАНИЕ
1. Область определения - R - все действительные.
разрывов нет - непрерывная.
2, Пересечение с осью Х - на интервале - нет.
3. На четность.
Y(-x) ≠ Y(+x) - функция ни четная ни нечетная.
4. Первая производная - экстремумы.
Y' = 3x²-12x+9 = 3*(x-1)(x-3)0
5. Монотонность.
Возрастает - Х∈(-∞,1]∪[3,+∞)
Убывает - Х∈[1,3]
6. Экстремумы
Ymax(1) = 5
Ymin(3) = 1
7. Вторая производная.
Y" = 6x-12 = 6(x-2)
8. Точка перегиба
Y"(2) =0
9.
Выпуклая - Х∈(-∞,2]
Вогнутая - X∈[2,+∞).
10. Значения на границах отрезка.
Y(0) =1
Y(4) = 5
х³-6х²+9х+1 на интервале Х∈[0,4].
ИССЛЕДОВАНИЕ
1. Область определения - R - все действительные.
разрывов нет - непрерывная.
2, Пересечение с осью Х - на интервале - нет.
3. На четность.
Y(-x) ≠ Y(+x) - функция ни четная ни нечетная.
4. Первая производная - экстремумы.
Y' = 3x²-12x+9 = 3*(x-1)(x-3)0
5. Монотонность.
Возрастает - Х∈(-∞,1]∪[3,+∞)
Убывает - Х∈[1,3]
6. Экстремумы
Ymax(1) = 5
Ymin(3) = 1
7. Вторая производная.
Y" = 6x-12 = 6(x-2)
8. Точка перегиба
Y"(2) =0
9.
Выпуклая - Х∈(-∞,2]
Вогнутая - X∈[2,+∞).
10. Значения на границах отрезка.
Y(0) =1
Y(4) = 5
Приложения:
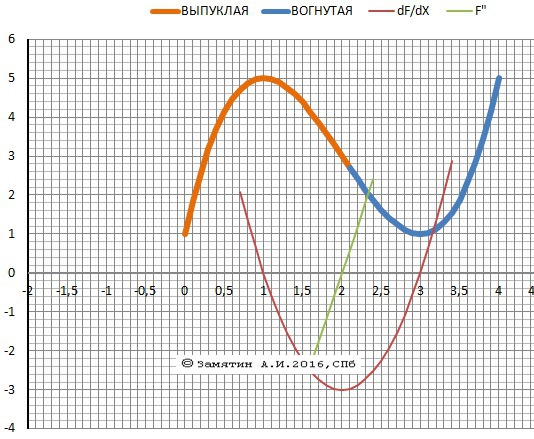
Ответил scenic
0
Спасибо огромное)
Новые вопросы
Биология,
2 года назад
Литература,
2 года назад
Биология,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад