Диагонали AC и BD ромба ABCD равны соответственно 12 и 9. Найдите расстояние от точки пересечения диагоналей ромба до боковой стороны.
Ответы на вопрос
Ответил Аноним
0
Диагонали ромба делятся точкой пересечения пополам. (Потому что диагонали параллелограмма так делятся, а ромб - то же самое что и параллелограмм) И угол между ними равен 90 градусов. Тогда пусть точка пересечения диагоналей - О, пусть А - левая вершина ромба, С - правая, В - верхняя, Д - нижняя. (Ну нарисуй так). Тогда АО=12:2=6, ОД=9:2=4.5. Тогда по теореме Пифагора находим АД. АД=ДС (т.к. АВСД - ромб), теперь есть треугольник АСД ,,,,,
в которой ты знаешь три стороны. У него есть угол Д, можно найти из теоремы косинусов. косД=(AD^2+DC^2-AC^2)/2AD*DC=(2AD^2-AC^2)/2AD^2=-AC^2/2AD^2
в которой ты знаешь три стороны. У него есть угол Д, можно найти из теоремы косинусов. косД=(AD^2+DC^2-AC^2)/2AD*DC=(2AD^2-AC^2)/2AD^2=-AC^2/2AD^2
Ответил eden01
0
Надо найти ОН.
АС=9, АО=ОС=4,5
ВД=12, ВО=ОД=6
АВ=корень из(6^2+4.5^2)=7,5
АН=(4,5)^2 / 7,5 = 2,7
ОН=корень из(4,5^2-2,7^2)=3,6см
АС=9, АО=ОС=4,5
ВД=12, ВО=ОД=6
АВ=корень из(6^2+4.5^2)=7,5
АН=(4,5)^2 / 7,5 = 2,7
ОН=корень из(4,5^2-2,7^2)=3,6см
Приложения:
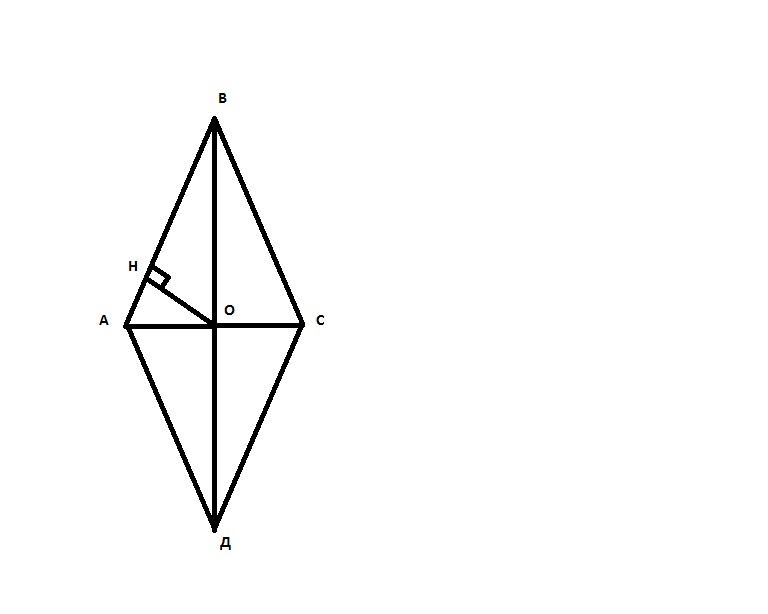
Новые вопросы