!!!!!!ДАЮ55БАЛОВСРОЧНО!!!!!!

Объяснение:

112. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів цього трикутника несуміжних з ним

41, 42, 43 - внутрішні кути трикутника

Нехай

41, 42 - внутрішні кути трикутника не суміжні із зовнішнім кутом трикутника, тоді

41+42=зовнішньому куту трикутника

41=89°, зовнішній кут трикутника = 146°- за

умовою задачі

89°+42=146°

42=146°-89°=57°

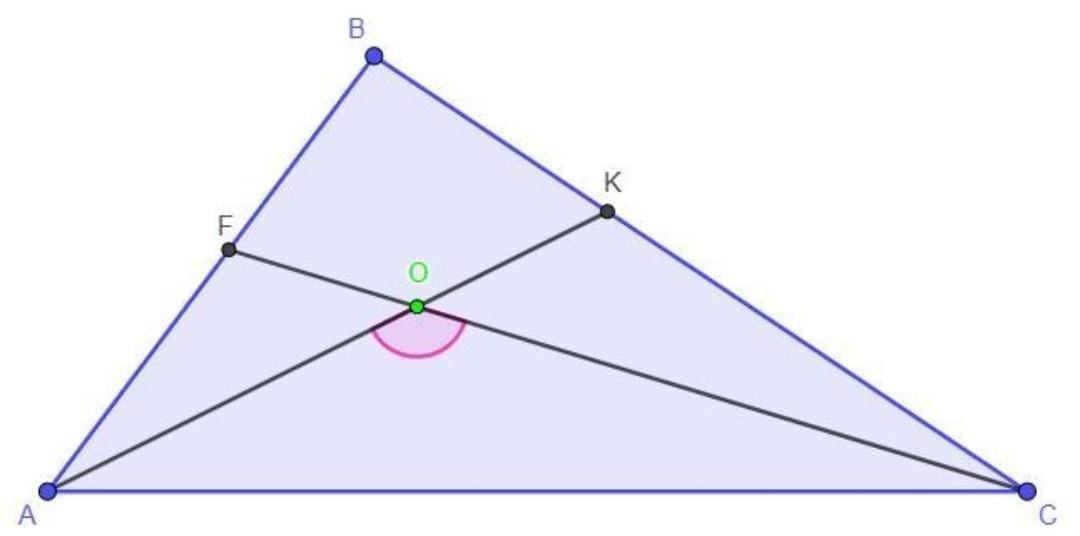
116.Дано: АК, CF - бісектриси; АК ∩ CF = O, ZAOC = 100°

Знайти: АBC - ?

Розв'язання:

За означенням бісектриса ділить кут навпіл, Отже ВАК = ∠CAK,

<BCF = ∠ACF.

За теоремою про суму кутів трикутника:

KAC + FCA + ∠AOC = 180° KAC + /FCA = 180° AOC = = 180° 100° = 80°.

<BAK + BCF = ∠CAK + ∠ACF, так як АК, CF - бісектриси за умовою.

Отже, кут ∠BAC + BCA = 2(BAK + BCF) = 2(CAK + ∠ACF) = = 2* 80° = 160°.

За теоремою про суму кутів трикутника:

BAC + BCA + ∠ABC = 180° ∠ABC = 180° - BAC BCA = = 180° - (BAC + ∠BCA) = 180°-160° 20°.

114- фото

120-теж фото

вроді все