Математика, вопрос задал kristina3268 , 2 года назад

Даю все свои баллы. Помогите пожалуйста. Решение неравенств

Приложения:

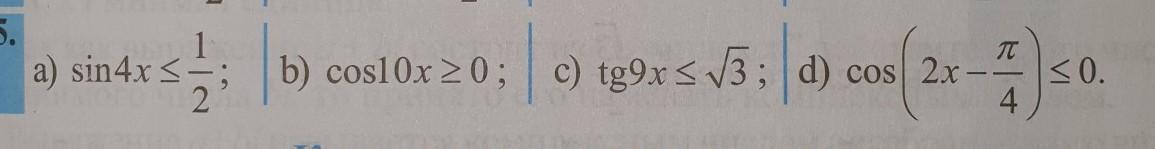
Ответы на вопрос

Ответил Miroslava227

1

Ответ:

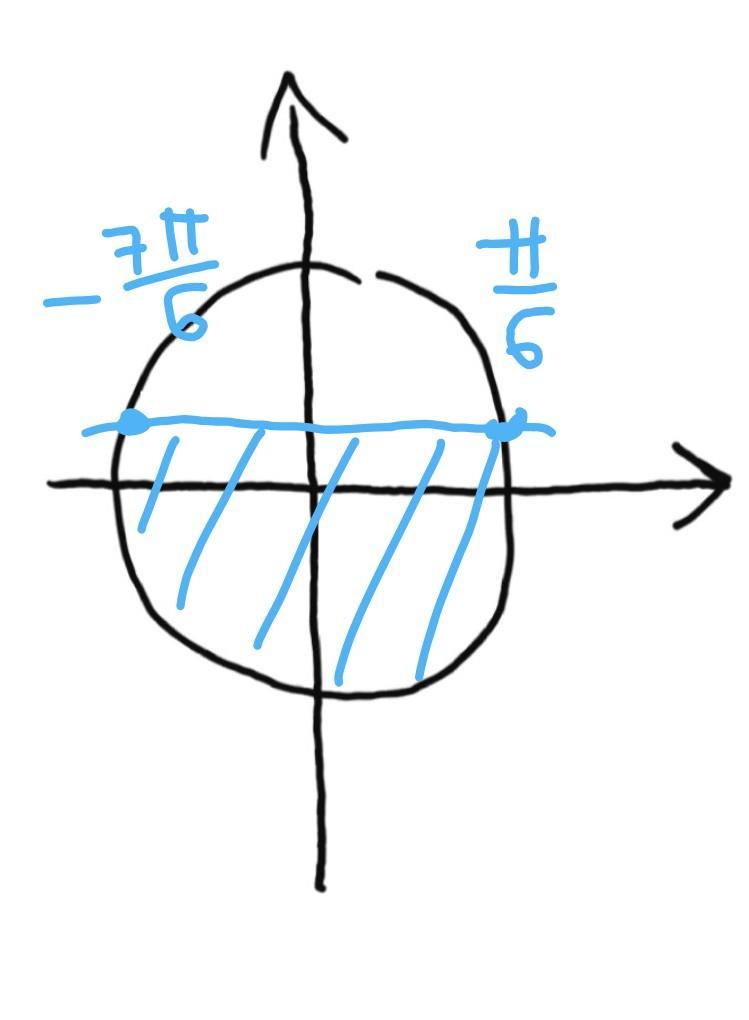
а

$\sin(4x) \leqslant \frac{1}{2} \\$

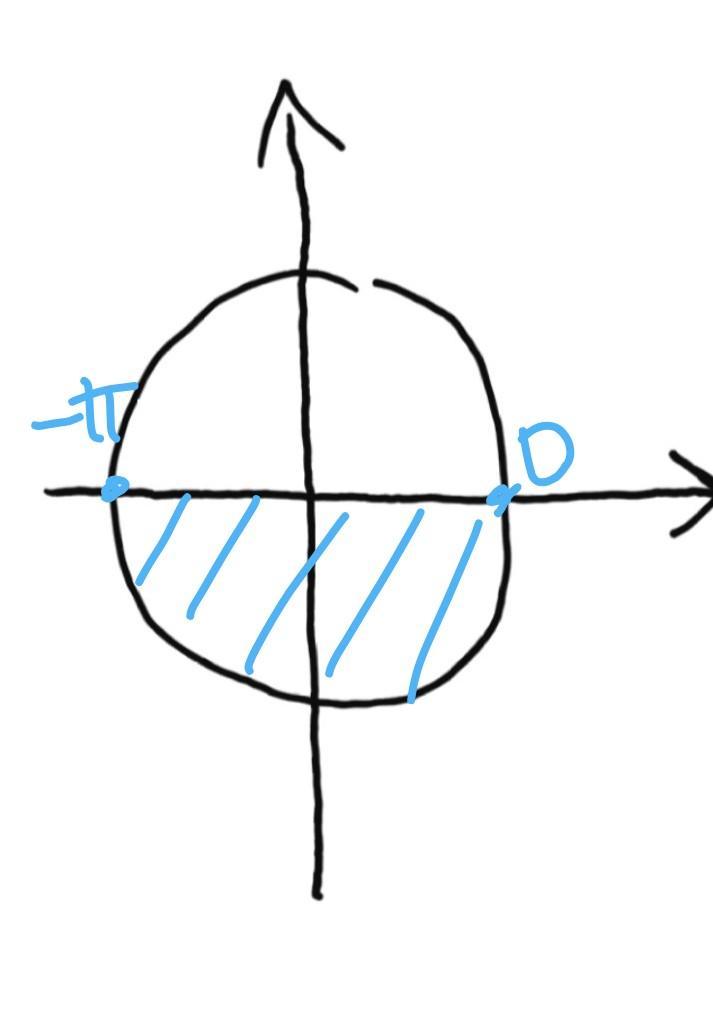
рисунок1

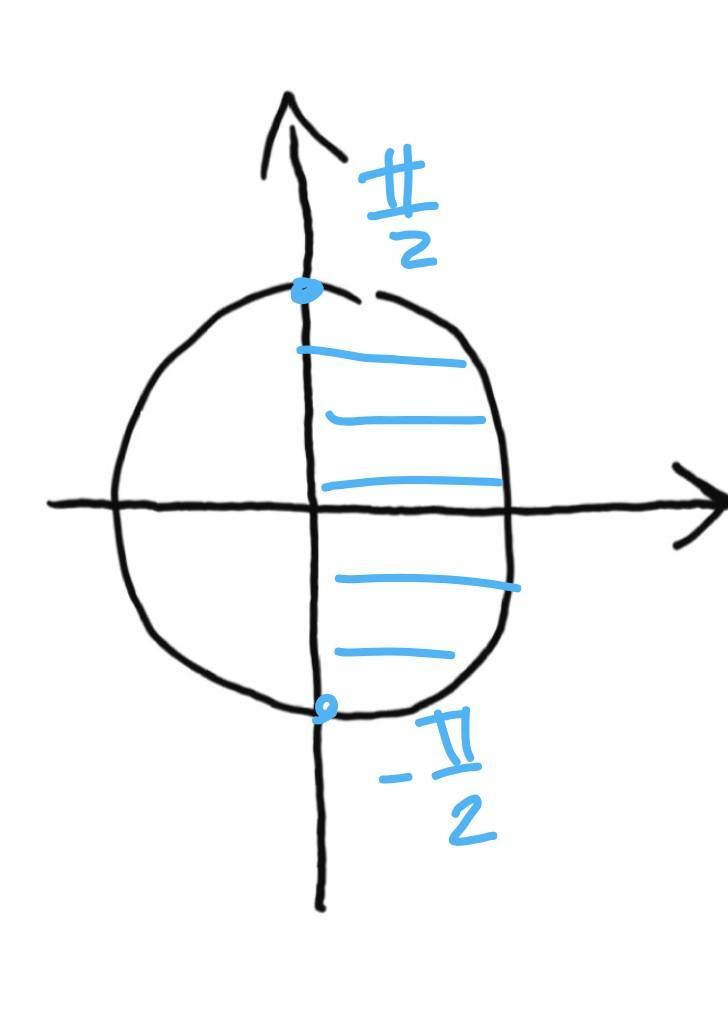
$4x\in( - \frac{7\pi}{6} +2 \pi \: n; \frac{\pi}{6} + 2\pi \: n) \\ x\in( - \frac{7\pi}{24} + \frac{\pi \: n}{2} ; \frac{\pi}{24} + \frac{\pi \: n}{2} ) \\ n\in \: Z$

б

$\cos(10x) \geqslant 0$

рисунок2

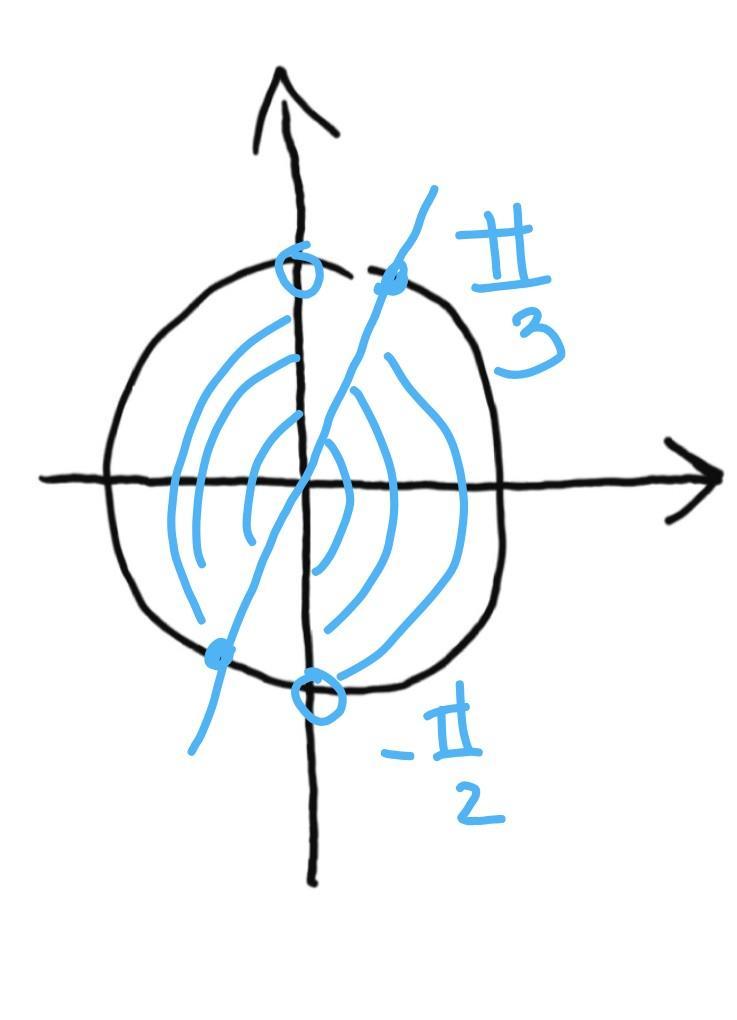
$10x\in( - \frac{\pi}{2} + 2 \pi \: n; \frac{\pi}{2} + 2\pi \: n) \\ x\in( - \frac{\pi}{20} + \frac{\pi \: n}{5} ; \frac{\pi}{20} + \frac{\pi \: n}{5} ) \\n \in \:Z$

в

$tg9x \leqslant \sqrt{3}$

рисунок3

$9x\in( - \frac{\pi}{2} + \pi \: n ;\frac{\pi}{3} + \pi \: n) \\ x\in( - \frac{\pi}{18} + \frac{\pi \: n}{9} ; \frac{\pi}{27} + \frac{\pi \: n}{9} ) \\n \in \:Z$

г

$\cos(2x - \frac{\pi}{4} ) \leqslant 0 \\$

рисунок4

$(2x - \frac{\pi}{4} )\in( - \pi + 2\pi \: n;2\pi \: n) \\ 2x\in( - \frac{3\pi}{4} + 2\pi \: n ;\frac{\pi}{4} + 2\pi \: n) \\ x\in( - \frac{3\pi}{8} + \pi \: n; \frac{\pi}{8} + \pi \: n) \\n \in \:Z$

Приложения:

kristina3268: Огромное спасибо!!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Другие предметы, 1 год назад

основное занятие у эскимосов...

Русский язык, 1 год назад

Из предложений 44—50 выпишите слово, в котором правописание суффикса определяется правилом: «В полных страдательных причастиях прошедшего времени пишется НН». –...

Українська мова, 2 года назад

ВЫБЕРИТЕ ПРАВИЛЬНУЮ БУКВУ 7 класс. Прийменник вказує на відношення мети в рядку : а)приїде в неділю б)заплакав від образи в)вітер з півночі г)прийшов на допомогу 4. Укажіть непохідні...

Математика, 2 года назад

В треугольнике KLM к стороне LM проведена высота, равная $5 \sqrt{3}$ Найди косинус угла L, если KL = 10.

Геометрия, 8 лет назад

В треугольнике РОК известны длины трех высот:РЕ=9, ОН=11, КС=10. Найдите расстояние от точки К до прямой ОР.

Математика, 8 лет назад

решите уравнение распишите действия пожалуйста...