Алгебра, вопрос задал abc348976 , 11 месяцев назад

Даю 50 балов , срочно помогите пожалуйста !!

Приложения:

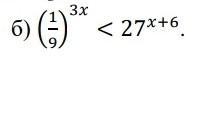
Ответы на вопрос

Ответил polarkat

1

$\left ( \cfrac{1}{9} \right )^{3x} < 27^{x+6}\Leftrightarrow 3^{-6x} < 3^{3x+18}\Leftrightarrow -6x < 3x+18\Leftrightarrow -9x < 18\Rightarrow x > -2$

Ответил hackkotik228

1

Відповідь: (-2; +∞)

Потрібно щоб були рівні основи

$(\frac{1}{9}) ^{3x} < 27^{x+6} \\ \\ (3^{-2}) ^{3x} < (3^{3})^{x+6} \\ \\ 3^{-2*3x} < 3^{3(x+6)} \\ \\ 3^{-6x} < 3^{3x+18}\\\\ -6x < 3x+18\\\\-6x-3x < 18\\\\-9x < 18\\\\\\9x > -18\\\\x > -\frac{18}{9} \\\\\\x > -2\\$

(-2; +∞)

hackkotik228: Кращу відповідь будь ласка

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 6 месяцев назад

Написать сочинение на тему "ChatGPT бесполезен"...

География, 6 месяцев назад

Визначити відповідні рівнини і заповнити таблицю.

Математика, 11 месяцев назад

Результат не залежить від задуманого числа, бо від суми задуманого числа і 100 відняли 37 і задумане число. Залишилось 100 37 = 63, тоді 63: 9 = 7. Цю задачу можна було розв'язати таким виразом:...

Алгебра, 11 месяцев назад

Знайдіть сторону АС ∆АВС, якщо: ...

Немецкий язык, 6 лет назад

Немецкое слово на тему свободное время. Нужно вставить две буквы I**fen...

Геометрия, 6 лет назад

(Рисунок, ДАНО, ЗНАЙТИ, РОЗВ'ЯЗУВАННЯ): При перетині двох прямих утворився кут 46 градусів. Знайти решту кутів.