Даю 50 баллов за простую задачу по геометрии,если подробно распишите решение!Спасибо!
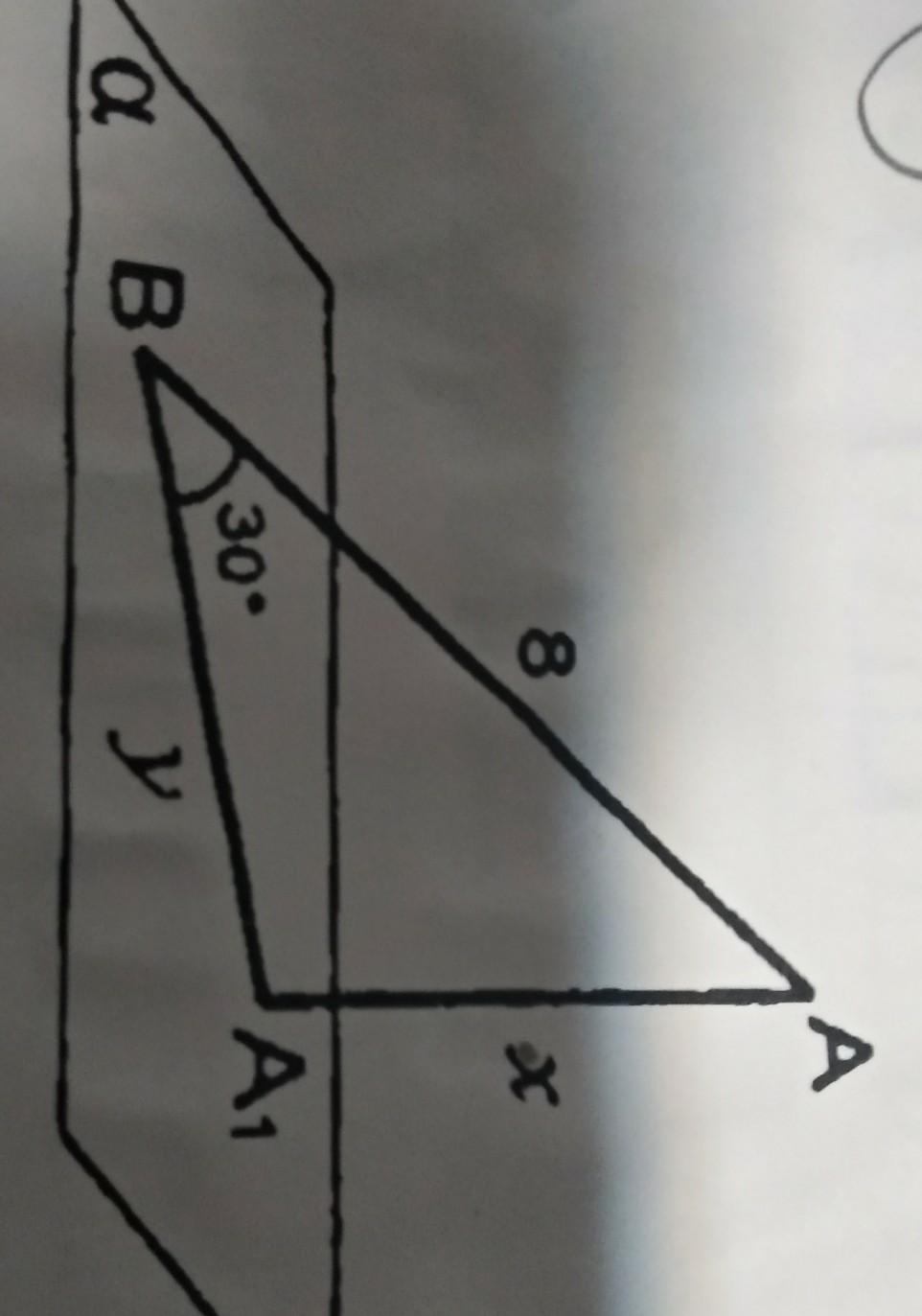
Треугольник АВА 1 прямоугольный.. АА1 перпендикуляр, АВ наклонная. Найти х и у.
Ответы на вопрос
сторона АА1 = х,
сторона ВА1 = у,
1.
так как треугольник прямоугольный, где АА1 - перпендиеуляр, то:
х = 1/2 * АВ (катет, лежащий против угла 30 градусов равен половине гипотенузы),
х = 1/2 * 8 = 4 ед.
2.
по теореме Пифагора:
АА1² + ВА1² = АВ²,
4² + у² = 8²,
у² = 8² - 4²,
у² = 64 - 16 = 48,
у = √48 = √(16*3),
у = 4√3 ед.
Ответ:
АА1= 4; А1В= 4корень(3)
Пошаговое объяснение:
1)Так как АА1 перпендикуляр к плоскости альфа, то он перпендикулярен всем прямым, находящимся в данной плоскости, АА1 перпендикулярен А1В.
2)Рассмотрим треугольник АА1В. Из пункта 1 мы знаем, что он прямоугольный, угол А1 = 90 градусов. По свойству прямоугольного треугольника с углом 30 градусов(сторона,лежащая напротив угла 30 градусов в прямоугольном треугольнике,равна половине гипотенузы),
АА1=1/2АВ, АА1= 4
3)По теореме Пифагора
А1В = корень(АВ^2-AA1^2)
А1В = корень(64-16) = корень(48) = 4корень(3)