Геометрия, вопрос задал catros , 8 лет назад

ДАЮ 50 БАЛЛОВ
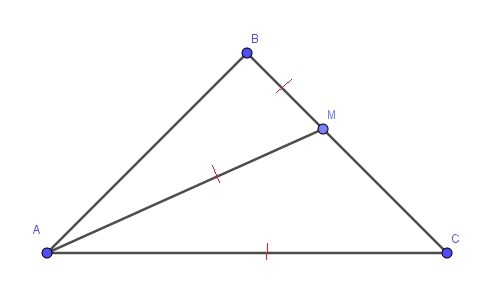
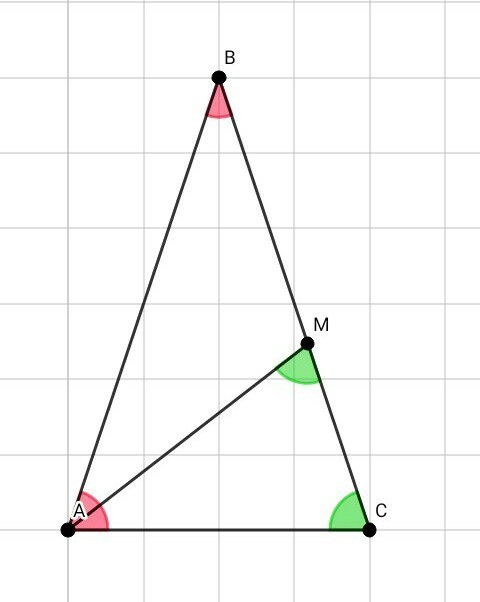
треугольник АВС равнобедренный с основанием АС. на стороне ВС отметили точку М, так что ВМ=АМ=АС. найдите углы треугольника АВС

Ответы на вопрос

Ответил Аноним

Обозначим углы при основании равнобедренного треугольника $tt ABC$ через α, то есть $tt angle A=angle C=alpha$ .

Рассмотрим треугольник $tt AMC$ , так как из условия $tt AC=AM$ , то треугольник $tt AMC$ - равнобедренный, следовательно, $tt angle ACM=angle AMC=alpha$

$tt angle BMA+angle AMC=180^circ$ откуда $tt angle BMA=180^circ-alpha$

Рассмотрим теперь треугольник ABM в нём $tt BM=AM$ , следовательно, треугольник $tt ABM-$ равнобедренный, значит $tt angle ABM=angle BAM$

$tt angle ABM+angle BAM+angle BMA=180^circ$ подставляя данные, получим $tt angle ABM+angle BAM+180^circ-alpha =180^circ$ откуда $tt angle ABM+angle BAM=alpha$

Углы при основании у равнобедренного треугольника ABM равны, следовательно, $tt angle ABM=angle BAM=dfrac{boldsymbol{alpha} }{2}$

Зная, что сумма углов треугольника АВС равна 180°, составим уравнение:

$tt alpha +dfrac{alpha }{2} +alpha =180^circ~~|cdot 2\ \ 2alpha +alpha +2alpha =360^circ\ \ 5alpha =360^circ\ \ alpha =72^circ$

Итак, $tt angle A=angle C=72^circ$ и $tt angle B=dfrac{alpha}{2} =dfrac{72^circ}{2}=36^circ$

Ответ: 72°; 72°; 36°.

Приложения:

Ответил Mihail001192

1) Обозначим угол АВС, угол при вершине равнобедренного треугольника, за Х, тогда
По условию ВМ = АМ →
∆ АВМ – равнобедренный

угол АВМ = угол ВАМ = х

2) угол АМС = угол ВАМ + угол АВМ – как внешний угол
Поэтому угол АМС = х + х = 2х

3) По условию АМ = АС →
∆ МАС – равнобедренный

угол АМС = угол АСМ = 2х

3) ∆ АВС – равнобедренный
Соответственно, угол ВАС = угол АСВ = 2х

Сумма всех углов в любом треугольнике всегда равна 180° :

угол ВАС + угол АВС + угол АСВ = 180°

2х + 2х + х = 180°

5х = 180°

х = 180°/5 = 36°

Значит, угол АВС = 36°
угол ВАС = угол АСВ = 2х = 2 × 36° = 72°

Также можно заметить, что
угол МАС = угол ВАС - угол ВАМ = 2х - х = х
Значит, АМ – биссектриса угла ВАС

ОТВЕТ: 72° ; 72° ; 36°

Приложения: