ДАЮ 50 БАЛЛОВ ПОЖАЛУЙСТА
Приложения:
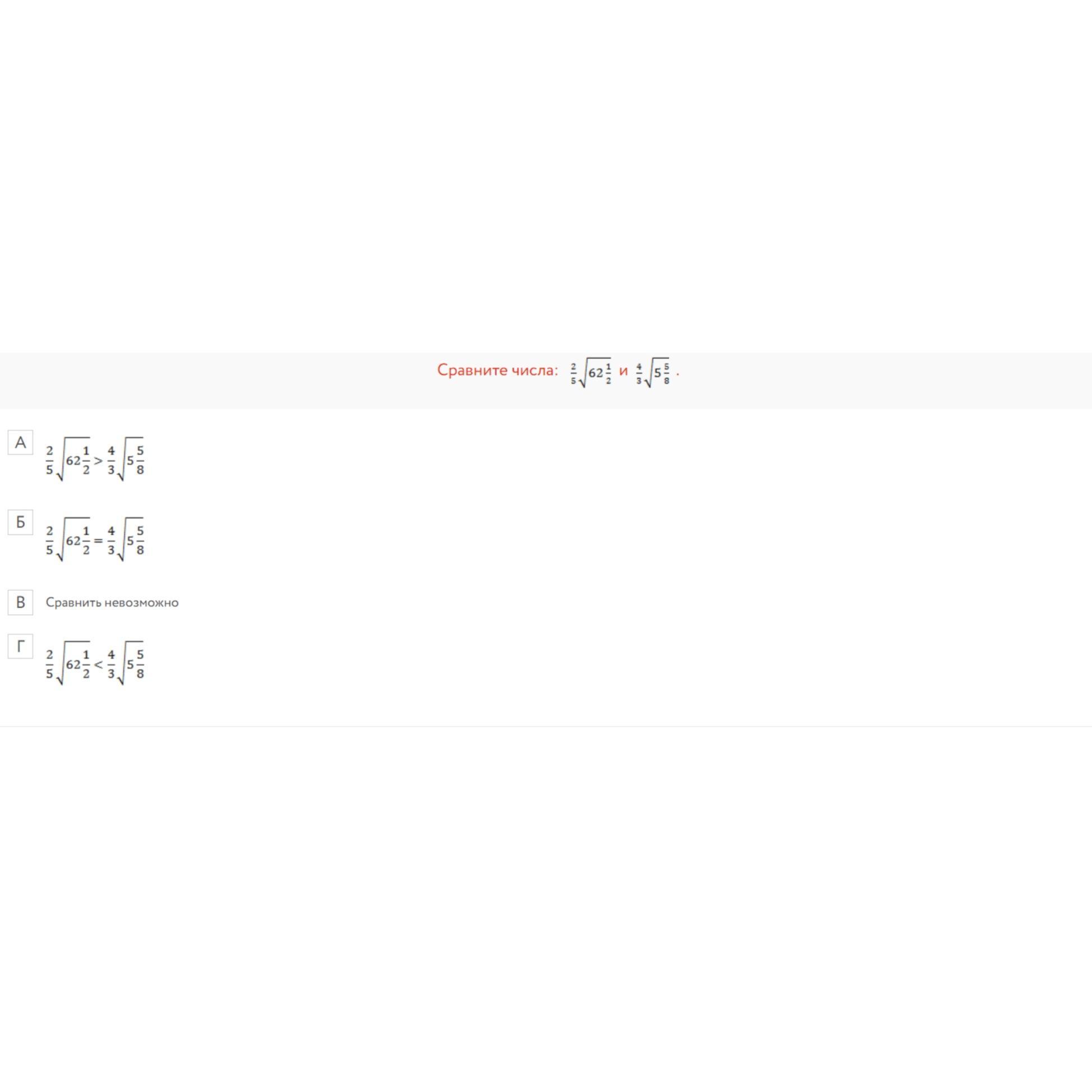
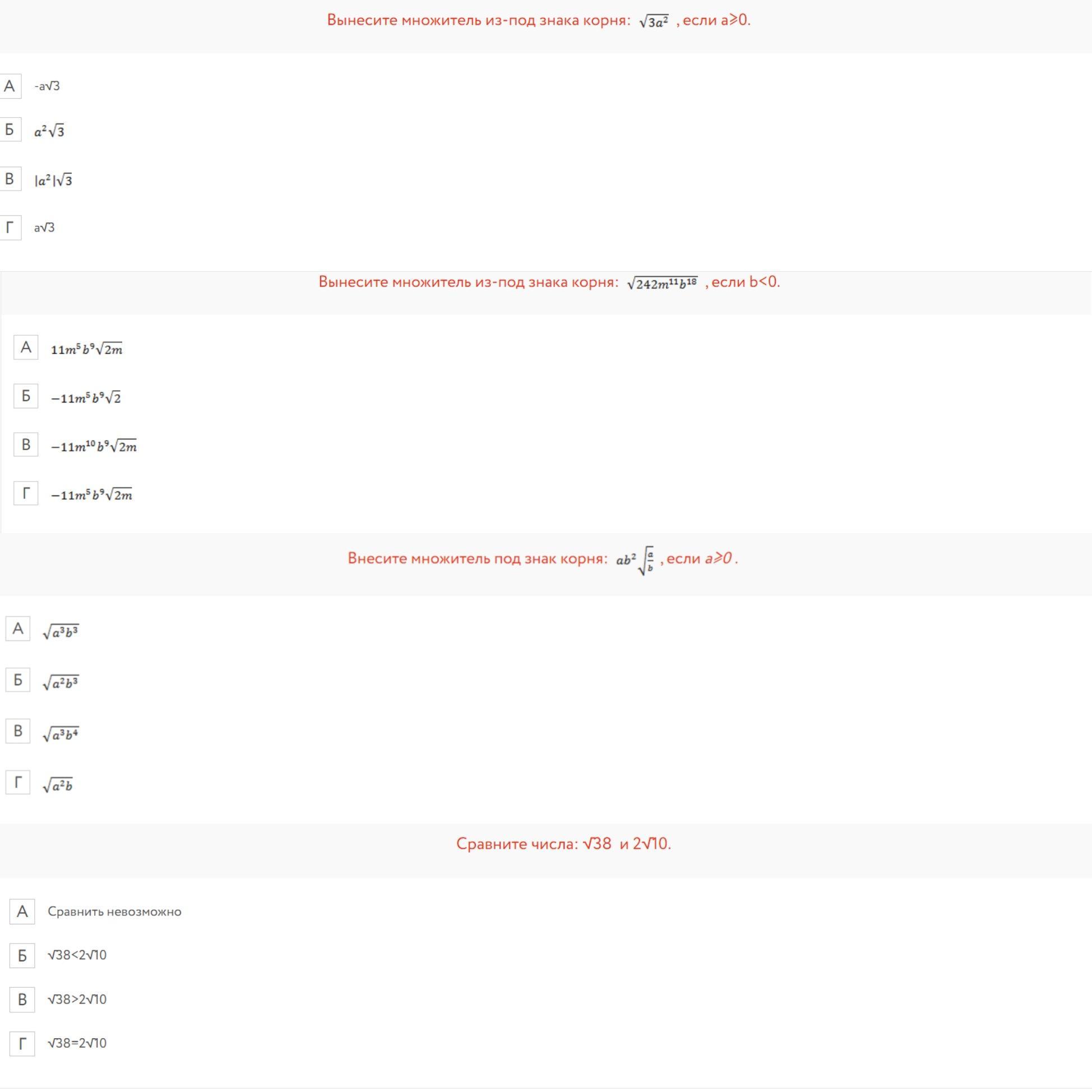
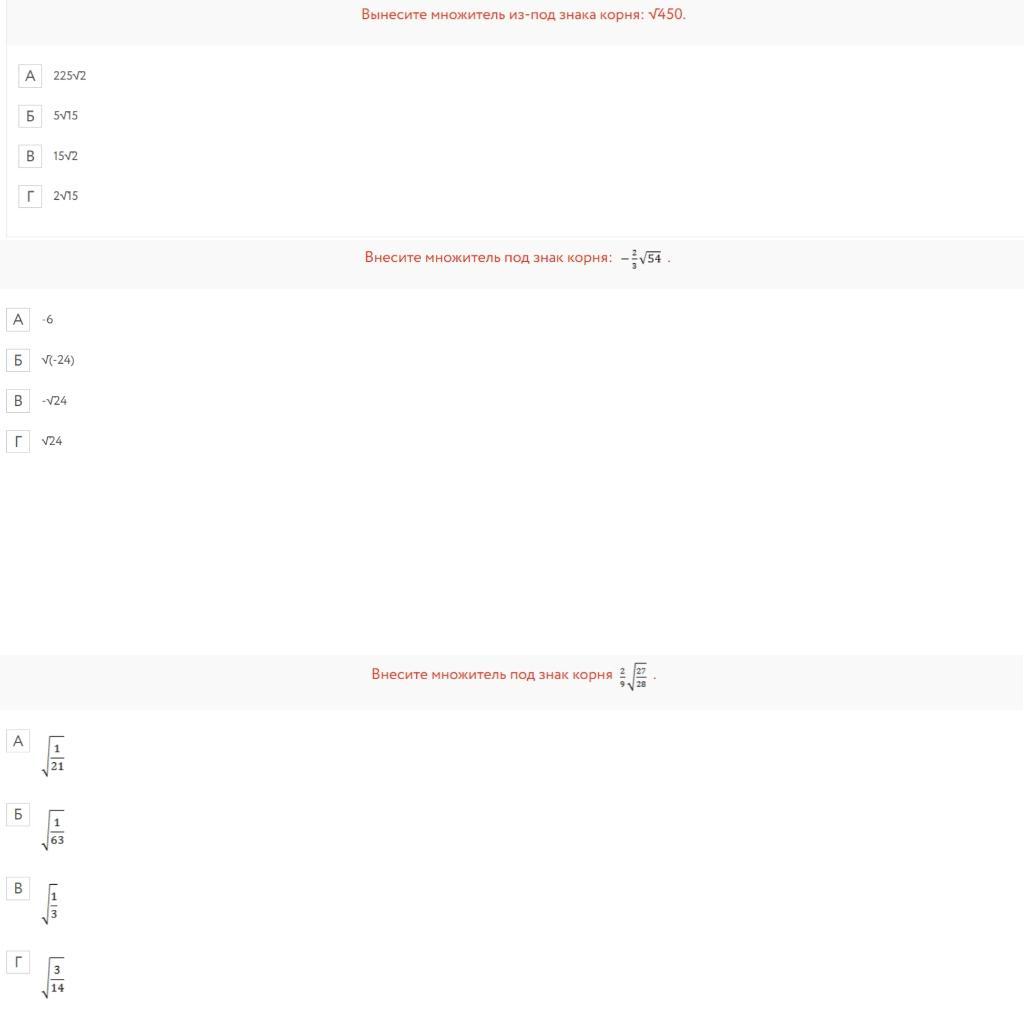
Ответы на вопрос
Ответил NNNLLL54
0
Ответ:
Новые вопросы