Даю 45 баллов!!! Помогите пожалуйста срочно!!Найдите уравнение касательной к графику функции f(x)=x^2-5x+3, если эта касательная параллельна прямой y=3x-1
Ответы на вопрос
Ответил olessyaabramova27
0
Ответ:
y=f(x0)+f′(x0)(x−x0)
в уравнении касательной x0 - координата точки касания. Она не известно, поэтому найдем ее. В условии сказано, что касательная параллельна прямой y=x−3. Если две прямые параллельны, то их угловые коэффициенты равны, т.е. угловой коэффициент касательной f′(x0) равен угловому коэффициенту прямой y=x−3, который равен k=1, т.е. получаем f′(x0)=1. Т.е. най необходимо найти производную функции и приравнять ее к одному и решить полученное уравнение
f′(x0)=(2x20–3x0)′=1=>4x0−3=1=>x0=1
Получили координату точки касания. Теперь найдем значение функции в этой точке
f(x0)=f(1)=2∗12−3∗1=−1
Подставляем полученный данные в уравнение касательной и получим
y=f(x0)+f′(x0)(x−x0)=−1+1∗(x−1)=>
y=x−2
Объяснение:
Приложения:
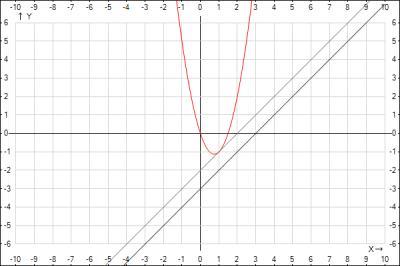
5d9wp5jifs:
Так в условии написано что y=3x-1 ,а не y=x-3
Новые вопросы
Русский язык,
1 год назад
Английский язык,
1 год назад
География,
6 лет назад
История,
6 лет назад
Математика,
8 лет назад