Даю 100 балов срочно геометрию!!!
Приложения:
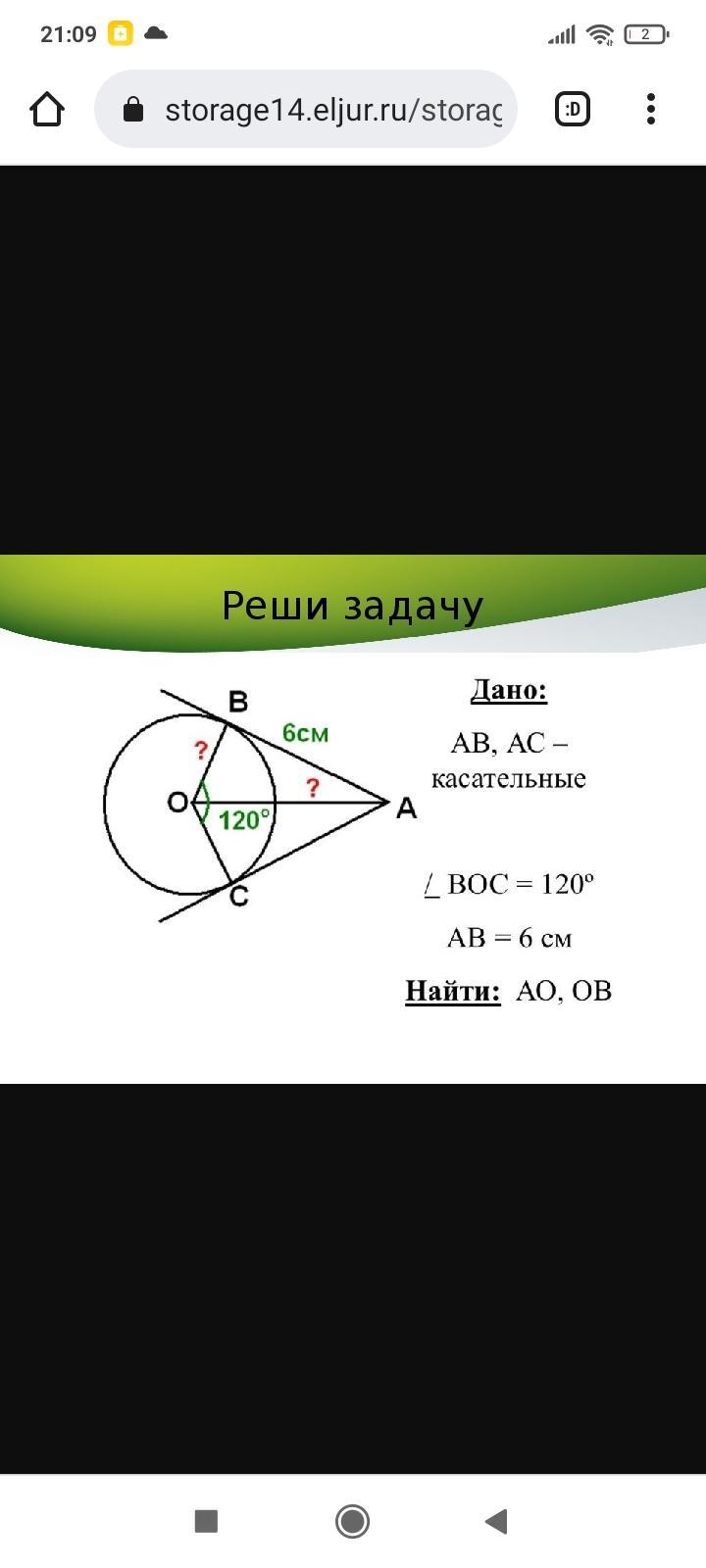
Ответы на вопрос
Ответил Аноним
0
по свойству отрезков касательных АВ=АС=6; ОА биссектриса, т.е. ОВ и ОС перпендикулярны касательным, то треугольники АОВ и АОС равны по катету - радиусам, и гипотенузе ОА, а раз ОА биссектриса, то угол ВОА равен 60°, угол ВАО=30°, тогда ОА=2*6=12/см/, ОВ=√(12²-6²)=6√3/см/
Ответил olgaua64
0
Відповідь:
Пояснення:
АО - биссектриса угла СОВ, из подобия прямоугольный треугольников АСО и АВО
Поэтому углы ВОА=60°, А=30° -> ОА=2ОВ
Если ОВ=х, то по теоремме Пифагора
ОВ²+ВА²=ОА²
х²+36=4х²
х²=36/3=12
х=2√3
ОВ=2√3
АО=4√3
Пояснення:
АО - биссектриса угла СОВ, из подобия прямоугольный треугольников АСО и АВО
Поэтому углы ВОА=60°, А=30° -> ОА=2ОВ
Если ОВ=х, то по теоремме Пифагора
ОВ²+ВА²=ОА²
х²+36=4х²
х²=36/3=12
х=2√3
ОВ=2√3
АО=4√3
Новые вопросы
Математика,
6 лет назад
Русский язык,
6 лет назад