даю 100 баллов за решение функции!!
Постройте график функции и определите, при каких значениях m
прямая y = m имеет с графиком одну или две общие точки
Приложения:
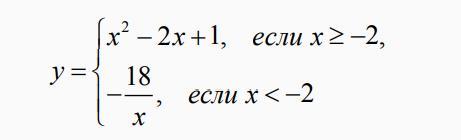
Ответы на вопрос
Ответил NNNLLL54
1
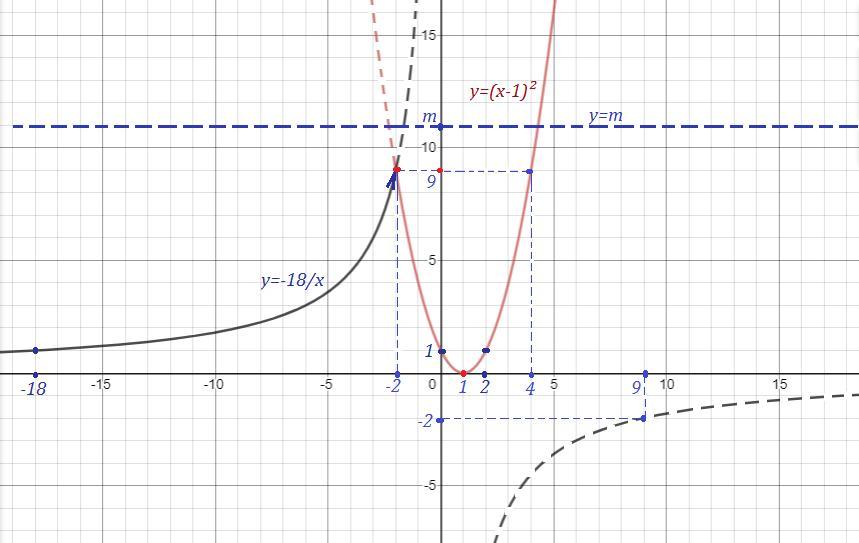
График начерчен сплошными линиями.
y=(x-1)² - парабола с вершиной в точке (1,0) , точка (-2,9) принадлежит графику, парабола чертится от точки (-2, 9) .
- гипербола, точка (-2,9) не принадлежит гиперболе, гипербола чертится до точки (-2,9).
Прямая y=m - прямая, параллельная оси ОХ, проходящая через точку (0,m) .
Одну точку пересечения прямая у=m с графиком заданной функции будет иметь при m=0 и m>9 .
Две точки пересечения прямая у=m с графиком заданной функции будет иметь при m=9 .
Приложения:
Новые вопросы
Математика,
1 год назад
Математика,
1 год назад
Другие предметы,
1 год назад
Обществознание,
6 лет назад
Английский язык,
6 лет назад