Алгебра, вопрос задал yulyarozenberg , 6 лет назад

ДАЮ 100 БАЛЛОВ!

Вычислите
Используя слова
1)ОДЗ
2) Представим правую часть как
Получим
С учётом ОДЗ, получим
Ответ:

Приложения:

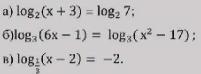
Аноним: Решу домашние задания и контрольные. В любое время и без баллов. Если интересует - напиши тут. Это задание решу после ответа)

yulyarozenberg: интересует

Аноним: Есть телеграмм? Можешь туда задания кидать

yulyarozenberg: телеграм kkrinzhyla

Ответы на вопрос

Ответил manyny06

1

Ответ:

решение смотри на фотографии

Приложения:

Ответил zinaidazina

1

a) $log_2(x+3)=log_27$

1) ОДЗ: $x+3 > 0= > x > -3$

2) Получим

$x+3=7$

$x=7-3$

$x=4$ $\in$ ОДЗ.

С учётом ОДЗ, получим корень $x=4$

Ответ: {4}

б) $log_3(6x-1)=log_3(x^{2} -17)$

1) ОДЗ: $\left \{ {{6x-1 > 0} \atop {x^2-17 > 0}} \right. < = > \left \{ {{x > \frac{1}{6} } \atop {x < -\sqrt{17};x > \sqrt{17} }} \right. < = > x > \sqrt{17} < = > x > 4,12$

2) Получим

$6x-1=x^{2} -17$

$x^{2} -6x-16=0$

$D=36-4*1*(-16)=36+64=100=10^2$

$x_1=\frac{6-10}{2}=-2$

$x_2=\frac{6+10}{2}=8$

С учётом ОДЗ, получим один корень $x=8$

Ответ: {8}

в) $log_{\frac{1}{3}}(x-2)=-2$

1) ОДЗ: $x-2 > 0= > x > 2$

2) Представим правую часть как

$log_{\frac{1}{3}}(x-2)=-2log_{\frac{1}{3}}(\frac{1}{3} )$

$log_{\frac{1}{3}}(x-2)=log_{\frac{1}{3}}(\frac{1}{3} )^{-2}$

$log_{\frac{1}{3}}(x-2)=log_{\frac{1}{3}}3^2$

$log_{\frac{1}{3}}(x-2)=log_{\frac{1}{3}}9$

$x-2=9$

$x=11$

С учётом ОДЗ, получим корень $x=11$

Ответ: {11}

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Сколько учился Лермонтов...

Українська мова, 1 год назад

утвори як найбільше нових слів із букв слова магазин...

Химия, 6 лет назад

ПОМОГИТЕ пожалуйстааа...

Українська мова, 6 лет назад

провідміняти: сім літаків, одна квітка, тридцять будинків, одинадцять днів, сто зошитів, сорок хмаринок, вісімсот шістдесят учнів.

Математика, 8 лет назад

Пожалуйста помогите...

Алгебра, 8 лет назад

Помогите срочно!!!Пожалуйста! Нужно с решением. Упростите выражение...