Алгебра, вопрос задал zhunisbekmansur , 11 месяцев назад

даю 100 баллов сроочнно полным ответом с подробными обьясниями

Приложения:

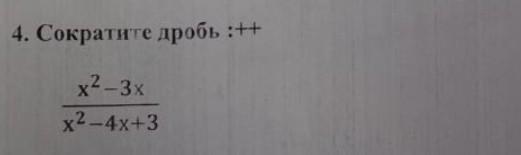
Ответы на вопрос

Ответил polarkat

0

$\cfrac{x^2-3x}{x^2-4x+3}=\cfrac{x(x-3)}{(x-1)(x-3)}=\cfrac{x}{x-1}$

Рассмотрим многочлен в знаменателе, а именно его коэффициенты. Воспользуемся одним интересным следствием из теоремы Виета: если сумма коэффициентов равна нулю, то первый корень равен единице, а второй $c/a$

$1+3-4$ действительно равно 0, а значит, первый корень единица, а второй три, от сюда и следует разложение в знаменателеи на множители

zhunisbekmansur: правильно?

polarkat: нет

zhunisbekmansur: без приколов это полный ответ .если нет можеж пожалуйста дать полный ответ

polarkat: Так без приколов, я ошибся

zhunisbekmansur: лдай полный ответ тогда

polarkat: Спасибо за жалобу)))

Ответил 7x8

0

Ответ:

$\displaystyle \frac{x}{x-1}$

Объяснение:

$\displaystyle \frac{x^2-3x}{x^2-4x+3}=\frac{x(x-3)}{x^2-x-3x+3}=\\\\\frac{x(x-3)}{x(x-1)-3(x-1)}=\frac{x(x-3)}{(x-1)(x-3)}=\frac{x}{x-1}$

ОДЗ:

$\displaystyle x\neq 3,\ x\neq 1$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Литература, 6 месяцев назад

чим пахла сільська бабуся у повісті "мій дідусь був черешнею" СРООООЧНОО...

Математика, 6 месяцев назад

8 h 40 min - 55 min=?

Английский язык, 11 месяцев назад

рецепт приготовления омлета на английском языке топик СРОЧНО!!

Русский язык, 11 месяцев назад

Соедините синонимичные исконно русские и ино- язычные существительные. При затруднениях обращайтесь к «Словарю иностранных слов». Бессмыслица Запас Неуспех, провал Клевета Нововведение Правило...

Литература, 6 лет назад

назвіть ОСНОВНУ ДУМКУ вірша Джона Донна Щоб мучить мене ДАЮ 100Б...

Биология, 6 лет назад

Помогите :) Назови три вида неперелетных птиц. Опиши их, опиши особенности питания, места гнездования, повадки птицы.