Математика, вопрос задал darktime11234 , 2 месяца назад

Даю 100 балів Терміново. Завдання на фото

Приложения:

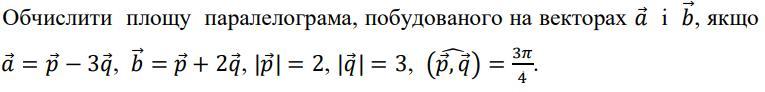
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Зная длины векторов a и b можно найти площадь параллелограмма , построенного на этих векторах, применив формулу :

$\bf S=|\overline{a}\times \overline{b}|=|\overline{a}|\cdot |\overline{b}|\cdot sin\alpha$ .

$\bf \overline{a}=\overline{p}-3\overline{q}\ \ ,\ \ \overline{b}=\overline{p}+2\overline{q}\ \ ,\ \ \ |\overline{p}|=2\ \ ,\ \ |\overline{q}|=3\ \ ,\ \ \varphi =\angle{(\overline{p},\overline{q})}=\dfrac{3\pi }{4}$

Найдём векторное произведение векторов а и b , применяя свойства векторного произведения .

$\bf \overline{a}\times \overline{b}=(\overline{p}-3\overline{q})\cdot (\overline{p}+2\overline{q})=\overline{p}\times \overline{p}+2\cdot \overline{p}\times \overline{q}-3\cdot \overline{q}\times \overline{p}-6\cdot \overline{q}\times \overline{q}=\\\\=\overline{p}\times \overline{p}+2\cdot \overline{p}\times \overline{q}+3\cdot \overline{p}\times \overline{q}-6\cdot \overline{q}\times \overline{q}=0+5\cdot \overline{p}\times \overline{q}-0=5\cdot \overline{p}\times \overline{q}$

Площадь параллелограмма равна

$\bf S=|\, \overline{a}\times \overline{b}|=|\, 5\cdot \overline{p}\times \overline{q}\, |= 5\cdot |\overline{p}|\cdot |\overline{q}|\cdot sin\varphi =5\cdot 2\cdot 3\cdot sin\dfrac{3\pi }{4}=\\\\=30\cdot \dfrac{\sqrt2}{2}=15\sqrt2$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 2 месяца назад

ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА...

Математика, 2 месяца назад

712. Периметр прямокутника 48 см. Периметр квадрата складае 2 периметра прямокутника. 3 Знайди площу квадрата.

Українська мова, 2 месяца назад

12. В одному зі складених речень визначити синтаксичну роль іменників. вот мои предложения Білоручка виказала високу ефективність у використанні завдань. Пустомеля виявила вражаючу спритність під...

Литература, 2 месяца назад

1. виконай тестові завдання. (дивіться фото) дуже срочно, треба сьогодні зробити!!!

Другие предметы, 6 лет назад

В какие геометрические фигуры можно вписать мотив «сияние»?

Другие предметы, 6 лет назад

ТЕХНОЛОГИЯ! В чём отличие техники резьбы сколышков от резьбы треугольников?