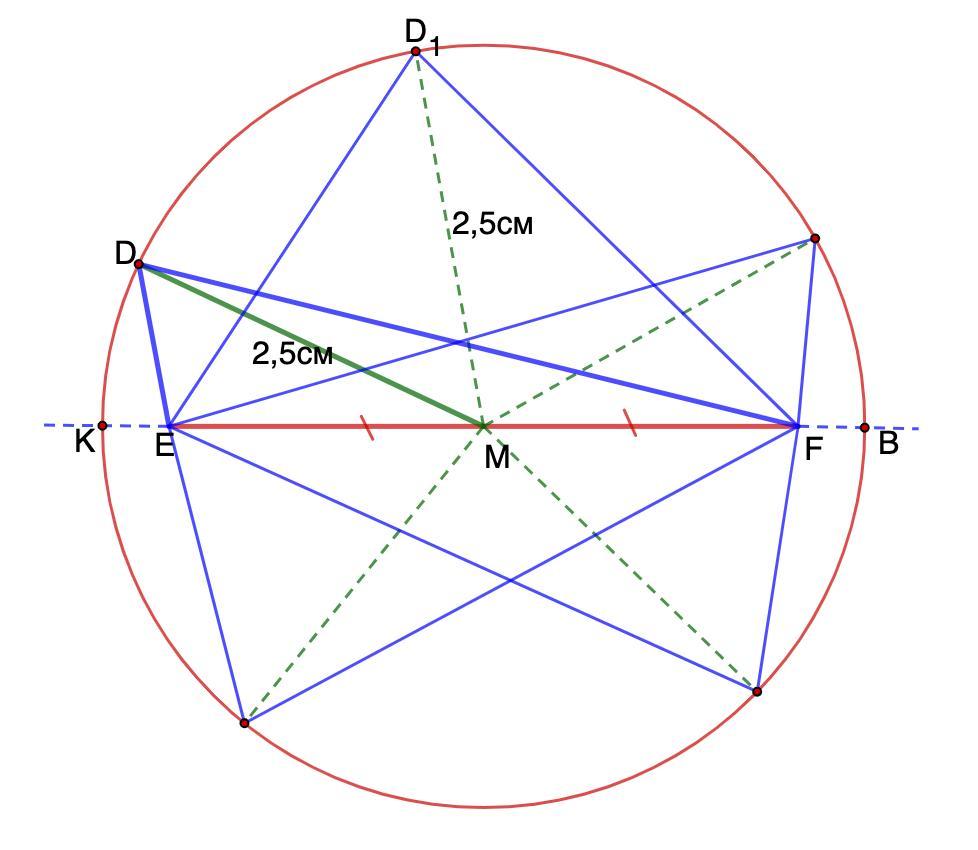
Даны точки E и F. Найдите ГМТ вершин D треугольников DEF таких, что медиана DM равна 2,5 см.

Ответ:

ГМТ вершин D треугольников DEF таких, что медиана DM равна 2,5 см  - это окружность с центром в точке М и радиусом DM = 2,5 см, кроме точек К и В.

Объяснение:

Требуется найти ГМТ вершин D треугольников DEF таких, что медиана DM равна 2,5 см.

• Геометри́ческое ме́сто то́чек (ГМТ) — определение геометрической фигуры как множества точек, обладающих некоторым свойством.

Отметим точки E и F и соединим их.

• Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Отметим точку М - середину EF.

Теперь из точки М проведем отрезок DM, равный 2,5 см. Соединим точку D с точками E и F.

Получили ΔEDF с медианой DM.

Из точки М мы можем провести множество отрезков длиной 2,5 см. Например MD₁ и др.

Все эти точки будут лежать на одном расстоянии от точки М.  

• Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.

⇒ ГМТ вершин D треугольников DEF таких, что медиана DM равна 2,5 см - это окружность с центром в точке М и радиусом DM = 2,5 см.

Исключением являются точки пересечения EF с окружностью, так как нарушается правило неравенства треугольника:

• Сумма двух сторон треугольника больше третьей стороны.

Таким образом:

ГМТ вершин D треугольников DEF таких, что медиана DM равна 2,5 см  - это окружность с центром в точке М и радиусом DM = 2,5 см, кроме точек К и В.