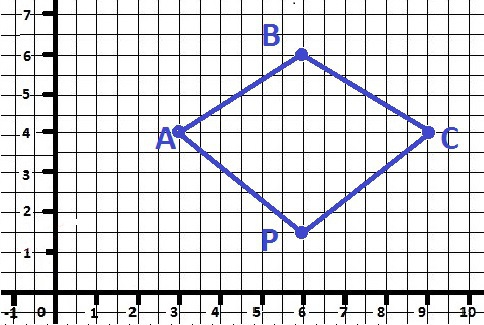
Даны точки А(3;4), В(6;6), С(9;4), Р(6;2). Докажите, что АВСР-параллелограмм

Построили на координатной плоскости четыре точки, соединили прямыми линиями и видим, что четырехугольник не только параллелограмм, а даже ромб.
Доказательство.
Стороны равны - гипотенузы треугольников с равными катетами.
Вх-Ах=6-3 = 3 и Сх-Рх= 9-6 = 3
Ву-Ау= 6-4 = 2 и Су-Ру= 4-2 = 2.
Стороны параллельны-  наклон отрезков одинаков.
k1 = ΔY/ΔX = (By-Ay)/(Bx-Ax) = 2/3 - наклон отрезка ВА.
k2 = (Cy-Py)/(Cx-Px) = 2/3 - наклон отрезка СР.
Аналогично для другой пары отрезков.
Настоящий параллелограмм и настоящий ромб.
ЧТД - что и требовалось доказать.