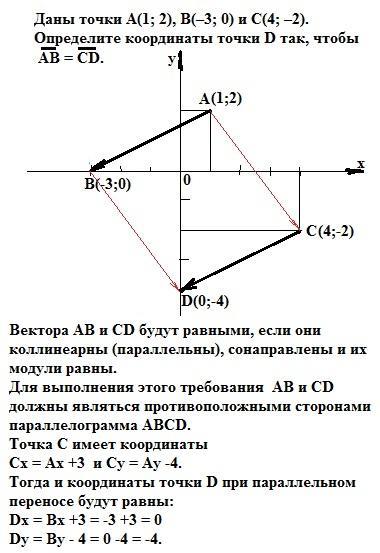
Даны точки А(1; 2), В(–3; 0) и С(4; –2). Определите координаты точки D так, чтобы

выполнялось равенство:

AB=CD​

Ответ:

D(0;-4).

Объяснение:

Вектора АВ и CD будут равными, если они коллинеарны (параллельны), сонаправлены и их модули равны.

Для выполнения этого требования  АВ и CD должны являться противоположными сторонами параллелограмма АВСD.

Точка С имеет координаты

Сx = Ax +3  и Cy = Ay -4.

Тогда и координаты точки D при параллельном переносе будут равны:

Dx = Bx +3 = -3 +3 = 0

Dy = By - 4 = 0 -4 = -4.

Проверка:

Найдем модули векторов:

|AB| = √((-3-1)²+(0-2)²) = √20.

|CD| = √((4-0)²+(-2-(-4))²) = √20.

Вектора АВ и CD равны, так как они коллинеарны (параллельны), сонаправлены и их модули равны.