Даны две параллельные плоскости α и β. Прямая АВ параллельна прямой CD. Точки А и В лежат в плоскости α, точки C и D лежат в плоскости β. Докажите, что существует плоскость, в которой лежат прямые АВ и СD.

Ответ:

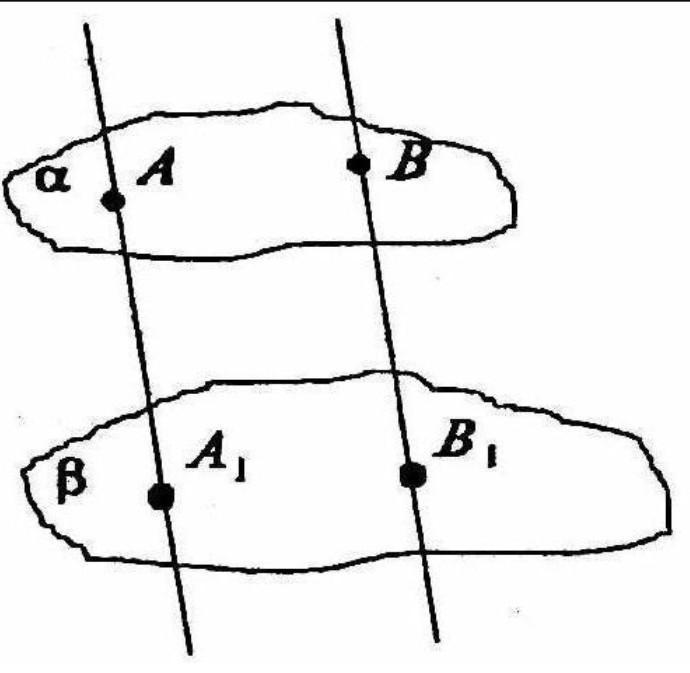
Проведем через параллельные прямые АА₁ и ВВ₁  плоскость. Она пересекает плоскость α и β по параллельным прямым AB и A₁B₁. Значит, четырехугольник AA₁B₁B — параллелограмм, т.к. AB||A₁B₁ и AA₁||BB₁.

У параллелограмма противоположные стороны равны, поэтому AB = A₁B₁ = m.

Если AB = m = 5, то A₁B₁ = m = 5;

если AB = m = 10, то A₁B₁ = m = 10;

если AB = m = 12,5, то A₁B₁ = m = 12,5;

и тд.

Объяснение:

Спасибо не мне а MistaB это он(а) ответил(а)