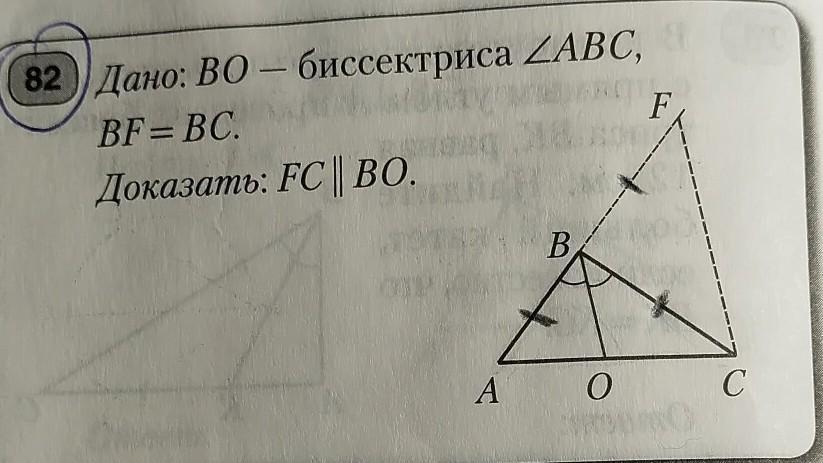
Дано: ВО- биссектриса угла ABC, BF = ВС. Доказать: FC || BO.
Приложения:
Ответы на вопрос
Ответил natalyabryukhova
2
Ответ:
Доказано, что FC || BO
Объяснение:
Доказать, что FC || BO.
Дано: ΔАВС.
ВО - биссектриса ∠АВС;
BF = BC.
Доказать: FC || BO.
Доказательство:
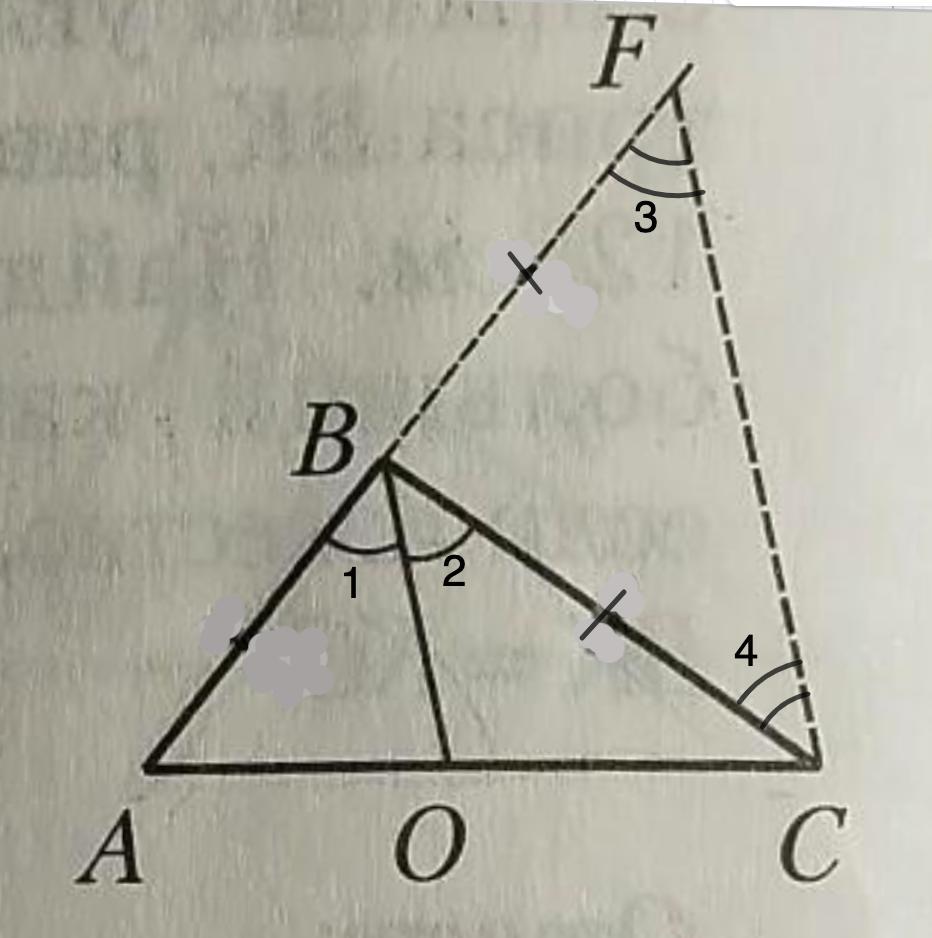
1. Рассмотрим ΔАВС.
- Смежные углы в сумме равны 180°.
⇒ ∠АВС = 180° - ∠FBC (смежные)
∠1 = ∠2 (ВО - биссектриса ∠АВС)
⇒ ∠1 = ∠2 = ∠АВС : 2 = (180° - ∠FBC) : 2 (1)
2. Рассмотрим ΔBFC.
BF = BC (условие)
⇒ ΔBFC - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠3 = ∠4
- Сумма углов треугольника равна 180°.
⇒ ∠3 + ∠4 = 180° - ∠ FBC
или
∠3 = ∠4 = (180° - ∠ FBC) : 2 (2)
3. Сравним полученные выражения (1) и (2).
∠1 = ∠2 = (180° - ∠FBC) : 2
∠3 = ∠4 = (180° - ∠ FBC) : 2
- Если правые части равенства равны, то равны и левые.
⇒ ∠1 = ∠2 = ∠3 = ∠4.
4. ∠2 = ∠4 - накрест лежащие при FC и OB и секущей ВС.
- Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
⇒ FC || OB
Приложения:
Новые вопросы