Дано вершини трикутної піраміди ABCD, А(– 4; 2; 1), В (– 1; 5; 4), С(– 2; – 4; 5), D(1; 2; –7)

Засобами векторної алгебри та аналітичної геометрії знайти площу грані АВС.

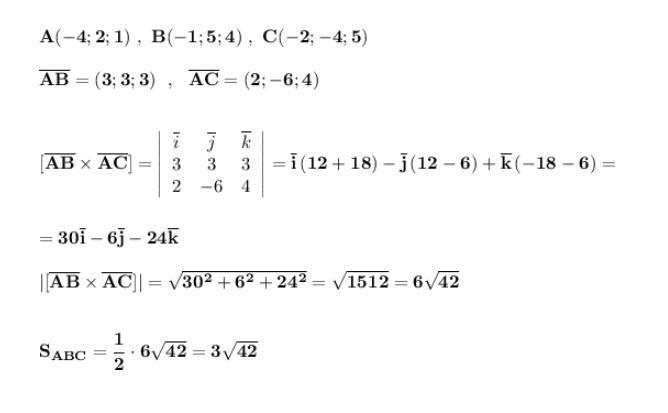
antongolos2006: Поясніть будь ласка, як прокоментувати ці дужки де i,j,k та як отримали числа з цих дужок( так, я не знаю як це рахуеться). і як прокоментувати момент де модуль і в ньому квадратні дужки?

NNNLLL54: В квадратных скобках пишут векторное произведения векторов [АВхАС ] . Затем записан определитель, а потом раскрывают определитель по 1 строке и получают строчку с i , j , k . Модуль | [ABхAC] | - это длина вектора , являющегося векторным произведением векторов АВ и АС . Это аналитическая геометрия и векторная алгебра .

antongolos2006: спасибо