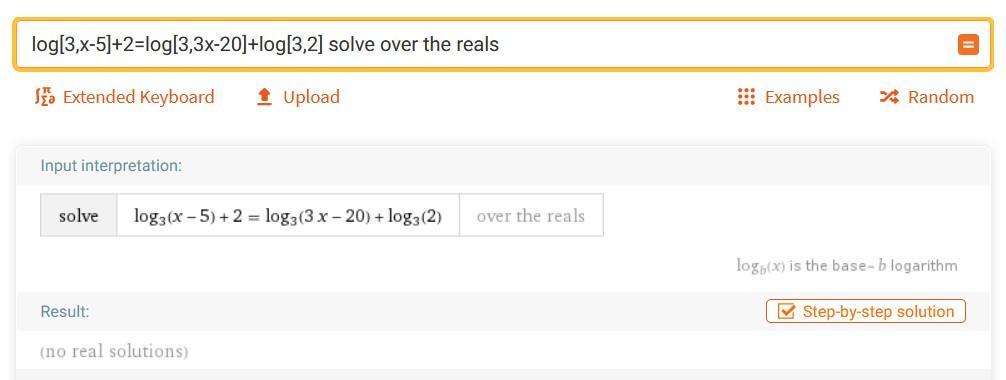
Алгебра, вопрос задал dfggdsfg0 , 1 год назад

Дано уравнение: $log_{3}(x-5)+2=log_{3}(3x-20)+log_32$
1. найдите область определения уравнения
2.решите уравнение

Ответы на вопрос

Ответил genius20

0

Выражение под логарифмом должно быть положительным, поэтому область определения:

$\begin{cases}x-5>0 \\ 3x-20>0 \end{cases} \Longrightarrow \quad \begin{cases}x>5 \\ x>\dfrac{20}{3}\end{cases} \Longrightarrow \quad x>\dfrac{20}{3}$

То есть $D(f) \in \left(\dfrac{20}{3}; + \infty\right)$

Решим уравнение:

$\log_3(x-5)+ \log_3 9-\log_3(3x-20)-\log_3 2=0\\\log_3\dfrac{9(x-5)}{2(3x-20)}=0\\\dfrac{9(x-5)}{2(3x-20)}=3^0=1\\9(x-5)=2(3x-20)\\9x-45=6x-40\\3x=5\\x=\dfrac{5}{3}$

Число $5/3<20/3$ , то есть вне области определения, поэтому корень не подходит.

Ответ: решений нет.

***

Если возникнут какие-либо вопросы — задавайте. Если мой ответ оказался полезен, нажимайте «спасибо» и отмечайте его как «лучший ответ».

P. S. На скриншоте проверка на компьютере.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Геометрия, 1 год назад

Обчисліть площу прямокутного трикутника, катети якого дорівнюють 9 см і 12 см S-?

Английский язык, 1 год назад

3 Wh-questions with to be Complete the questions for the answers given. 1 2 3 4 6 5 Q: Where were you yesterday? A: We were at the cinema. Q: When was he in Istanbul? A: He was there in 1998. 9: Why...

Английский язык, 1 год назад

Допоможіть будь-ласка із завданнями 3 і 4, буду вдячна...

Українська мова, 1 год назад

Укр мова Заболотний 6 клас самостійна робота по числівнику...

Английский язык, 6 лет назад

8. Which tense forms are correct? The exchange students ... with a host family for a year. 1. live 2. lived 3. will live 4. lives no...

Английский язык, 6 лет назад

123. Заповніть пропуски відповідною формою дієслова. 1) had better; 2) after being had; 3) had; 4) had had; 5) has; 6) are having; 7) has had; 8 ) without having; 9) had been; 10) being had; 11)...