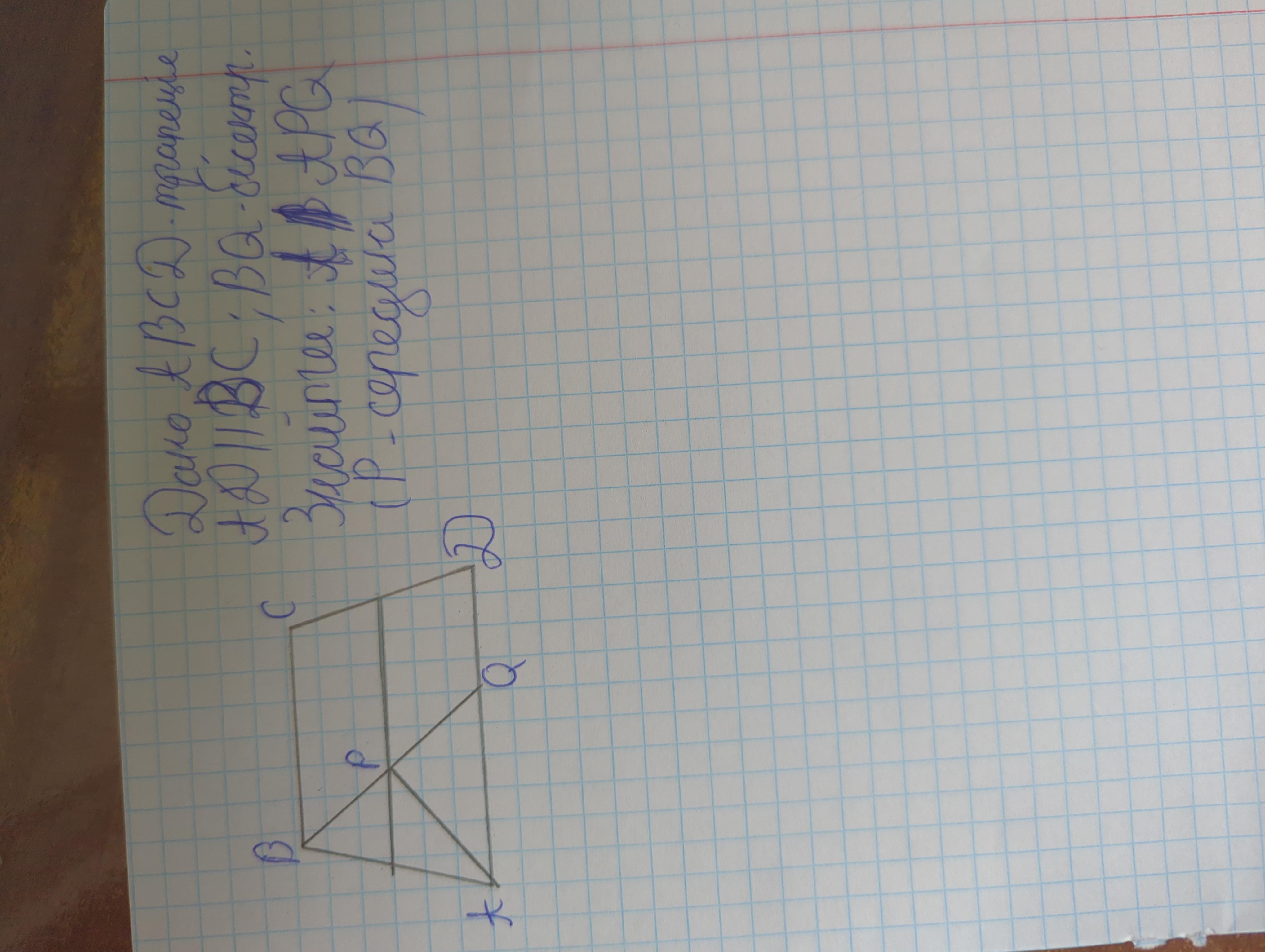
Дано трапецію ABCD AD||BC Відомо що бісектриса кута АBC перетинає середню лінію цієї трапеції в т. Р а основу AD в т. Q знайдіть величину кута APQ (т. P середина BQ)
Приложения:

Ответы на вопрос
Ответил rootoor
0
Відповідь:
Розглянемо трикутник ABC. Оскільки бісектриса кута ABC ділить кут навпіл, то кут ABP дорівнює куту BCQ.
Також, оскільки точка P є серединою відрізка BQ, то кути BPQ і BQP рівні.
Отже, трикутник BPQ є рівнобедреним, а кути BPQ і BQP рівні 60°.
Кут ABP дорівнює куту APQ, а кут ABP дорівнює куту BCQ, отже кут APQ дорівнює куту BCQ, а кут BCQ дорівнює 60°.
Відповідь: кут APQ дорівнює 60°.
Доказ:
ABP = BCQ
BP = BQ
Тому трикутник BPQ є рівнобедреним, а кути BPQ і BQP рівні:
BPQ = BQP = 60°
Також, кут ABP дорівнює куту APQ:
ABP = APQ
Отже, кут APQ дорівнює куту BCQ, а кут BCQ дорівнює 60°:
APQ = BCQ = 60°
Пояснення:
vinogradovtimur7:
Либо у меня не правильное построение, либо это не оно. Можешь своё построение скинуть?
Новые вопросы
Литература,
11 месяцев назад
Українська література,
11 месяцев назад
Информатика,
11 месяцев назад
Литература,
6 лет назад
Английский язык,
6 лет назад