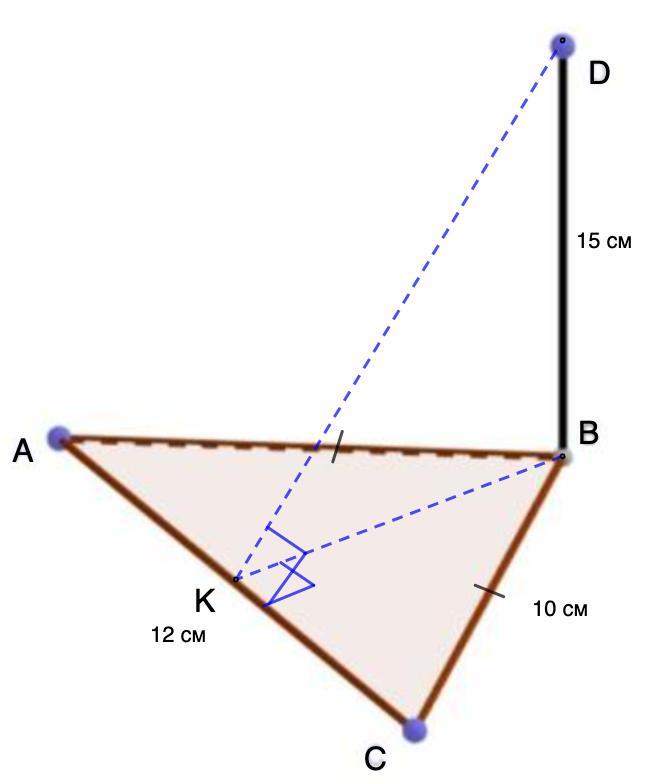
Дано: рівнобедрений трикутник ABC, AB = BC =10 см; АС = 12 см; DВ = 15 см, DB перпендикулярно площині трикутника. Знайти відстань від т. D до сторони АС.

Ответ:

Расстояние от точки D до стороны АС равно 17 см.

Объяснение:

Дано: равнобедренный треугольник ABC, AB = BC =10 см; АС = 12 см; DВ = 15 см, DB перпендикулярно плоскости треугольника. Найти расстояние от точки D до стороны АС.

Дано: ΔАВС - равнобедренный;

DB ⊥ АВС;

AB = BC =10 см; АС = 12 см; DВ = 15 см;

Найти: расстояние от D до АС.

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ искомый отрезок DK.

DK ⊥ AC.

• Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

⇒ ВК ⊥ АС.

Рассмотрим ΔАВС - равнобедренный.

ВК - высота.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ АК = КС = 12 : 2 = 6 (см)

Рассмотрим ΔКВС - прямоугольный.

По теореме Пифагора найдем ВК:

ВК² = ВС² - КС² = 100 - 36 = 64   ⇒   ВК = √64 = 8 (см);

Рассмотрим ΔKDВ - прямоугольный.

ВК = 8 см; DB = 15 см.

По теореме Пифагора найдем DK:

DK² = BK² + DB² = 64 + 225 = 289   ⇒   √289 = 17 (см)

Расстояние от точки D до стороны АС равно 17 см.

#SPJ1