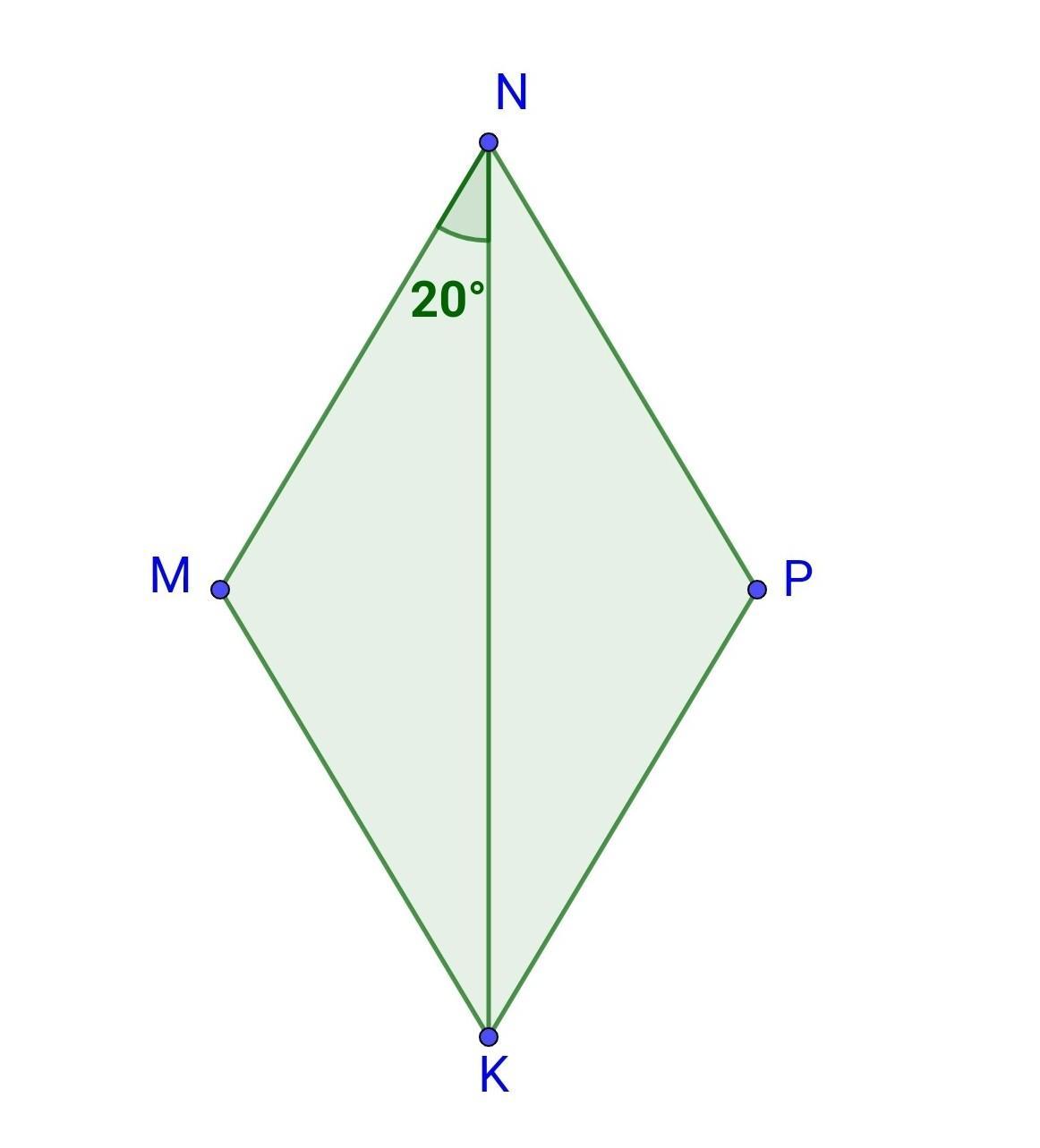
дано: MNPK - ромб. кут KNM = 20°. знайти менший кут ромба​

Ответ:

Менший кут ромба дорівнює 40°.

Объяснение:

Дано: MNPK - ромб. кут KNM = 20°.

Знайти: менший кут ромба

Розв'язання

За умовою MNPK - ромб, NK - діагональ.

За властивістю діагоналей ромба маємо:

∠KNM=∠KNP=20°.

Звідси маємо:

∠MNP=2•∠KNM=2•20°=40°.

За властивістю кутів ромба, прилеглих до однієї сторони, маємо:

∠MNP+∠M=180°

∠M=180°-∠MNP=180°-40°=140°.

За властивістю протилежних кутів ромба:

∠М=∠Р=140°, ∠MNP=∠MKP=40°.

Отже, менший кут ромба дорівнює 40°.

Відповідь: 40°.

#SPJ1