Дано конус, висота якого дорівнює 7 см, а кут при основі осьового перерізу - 30°. Встановити відповідність між елементами конуса (1 - 3) та їх числовими значеннями (А - Г) 1. Радіус основи конуса 2. Твірна конуса 3. Діаметр основи конуса А) 28 см; Б) 7 корінь 3 см; В) 14 корінь 3 см; Г) 14 см

Ответ:

1   →   Б

2   →   Г

3   →   В

Объяснение:

Дан конус, высота которого равна 7 см, а угол при основании осевого сечения - 30°. Установить соответствие между элементами конуса (1 - 3) и их числовыми значениями (А - Г)

1. радиус основания конуса 2. образующая конуса 3. диаметр основания конуса

А) 28 см; Б) 7√3 см; В) 14√3 см; Г) 14 см

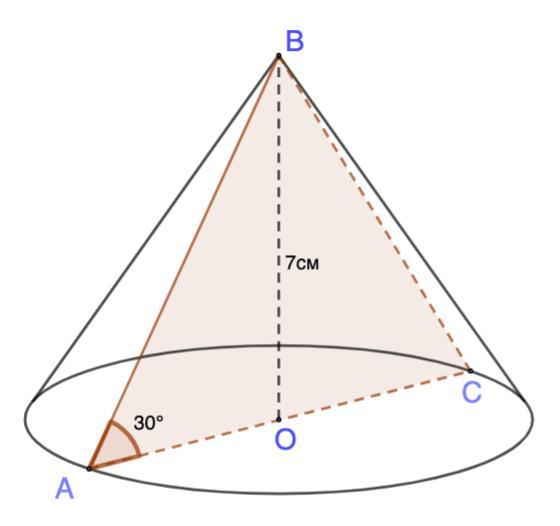
Дано: конус;

ΔАВС - осевое сечение;

ВО = 7 см - высота; ∠ВАС = 30°

Найти: 1. R основания; 2. АВ; 3. диаметр основания.

Решение:

1. Рассмотрим ΔАВО - прямоугольный.

ВО = 7 см; ∠ВАС = 30°

• Тангенс угла - отношение противолежащего катета к прилежащему.

Радиус основания равен 7√3 см.

2. Найдем образующую АВ.

• Теорема Пифагора:
• Квадрат гипотенузы равен сумме квадратов катетов.

⇒   АВ² = ВО² + АО² = 49 + 147 = 196   ⇒   АВ = 14 см

Образующая конуса равна 14 см.

3. Найдем диаметр.

• Диаметр равен двум радиусам.

АС = 7√3 · 2 = 14√3 (см)

Диаметр равен 14√3 см.

#SPJ1