Дано:
Довжина = 12 Пі
Довжина сторони 4 кореня із 3
Знайти: альфа, бетта, гамма
Як розв'язати цю задачу?
Ответы на вопрос
Ответил Ellenochka
0
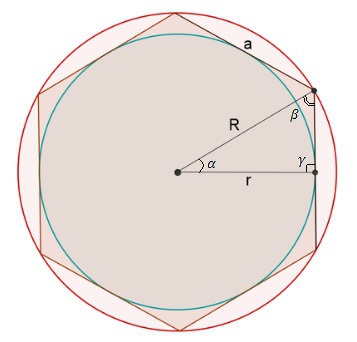
за розрахунком - це коло вписане в 6-кутник. =)
r - радіус вписаного кола
L - довжина кола
a - сторона багатокутника
n - кількість сторін многокутника
α, β, γ - кути за малюнком (хоч я незнаю, які вони у тебе за умовою)
L = 2πr =>
 - довжина радіуса
- довжина радіуса

 - сторін правильного многокутника
- сторін правильного многокутника
 °
°
 °
°
γ = 90° - оскільки r ⊥ a.
Так мажливо й радіус описаного кола знайти R=4√3
все =)
r - радіус вписаного кола
L - довжина кола
a - сторона багатокутника
n - кількість сторін многокутника
α, β, γ - кути за малюнком (хоч я незнаю, які вони у тебе за умовою)
L = 2πr =>
γ = 90° - оскільки r ⊥ a.
Так мажливо й радіус описаного кола знайти R=4√3
все =)
Приложения:
Новые вопросы