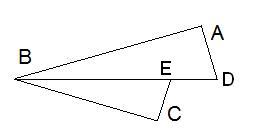
Геометрия, вопрос задал Аноним , 1 год назад

Дано, что BE — биссектриса угла ABC. BA⊥ADиEC⊥BC.

Найди BE, если AD= 12 см, BA= 16 см, EC= 2,4 см.

Сначала докажи подобие треугольников.

∢ =∢C= °∢C D=∢DB

,т.к. E− биссектриса}⇒ΔDBA∼ΔEBC по двум углам (по первому признаку подобия треугольников).

Приложения:

Ответы на вопрос

Ответил darkness88lucifer

Ответ:

это подставляй в окошки

<A=<C=90'

<CBD=<DBA

это просто решение

$bd = \sqrt{ {ab}^{2} + {ad}^{2} } = \sqrt{ {12}^{2} + {16}^{2} } = \sqrt{400} = 20$

$\frac{be}{bd} = \frac{ec}{ad } \\ be = \frac{ec \times bd}{ad} = \frac{2.4 \times 20}{12} = \frac{24}{6} = 4$

а это опять вписывай be=4

Новые вопросы

Английский язык, 1 год назад

Французский язык, 1 год назад

Обществознание, 1 год назад

Химия, 1 год назад

Литература, 6 лет назад

Геометрия, 6 лет назад