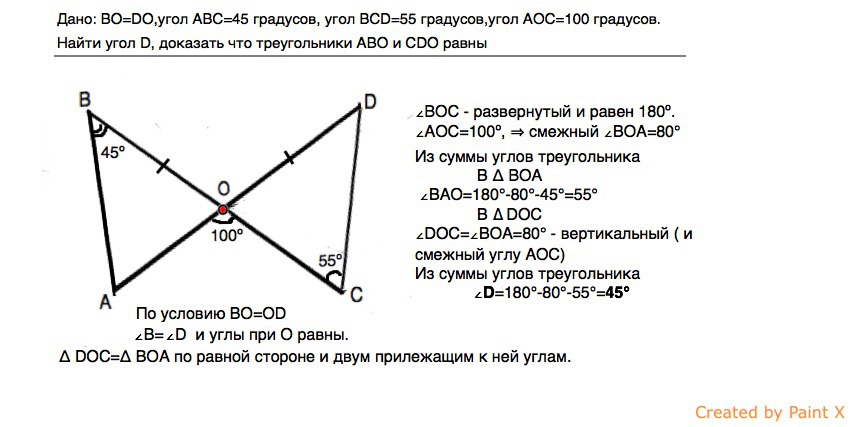
Дано: BO=DO,угол ABC=45 градусов, угол BCD=55 градусов,угол АОС=100 градусов.Найти угол D,доказать что треугольники АВО и СDO равны
Ответы на вопрос
Ответил Hrisula
0
Прямые ВС и АD пересекаются в точке О.
Следовательно, ∠ВОС - развернутый и равен 180º.
∠АОС=100º, ⇒ смежный ∠ВОА=80°
Тогда из суммы углов треугольника
В Δ ВОА
∠ВАО=180°-80°-45°=55°
В ∆ DOC
∠DOC=∠ВОА=80° - вертикальный ( и смежный углу АОС_.
Тогда из суммы углов треугольника
∠D=180°-80°-55°=45°
По условию ВО=ОD
Δ DOC=Δ ВОА по равной стороне и двум прилежащим к ней углам.
Следовательно, ∠ВОС - развернутый и равен 180º.
∠АОС=100º, ⇒ смежный ∠ВОА=80°
Тогда из суммы углов треугольника
В Δ ВОА
∠ВАО=180°-80°-45°=55°
В ∆ DOC
∠DOC=∠ВОА=80° - вертикальный ( и смежный углу АОС_.
Тогда из суммы углов треугольника
∠D=180°-80°-55°=45°
По условию ВО=ОD
Δ DOC=Δ ВОА по равной стороне и двум прилежащим к ней углам.
Приложения:
Новые вопросы
История,
6 лет назад
Математика,
9 лет назад