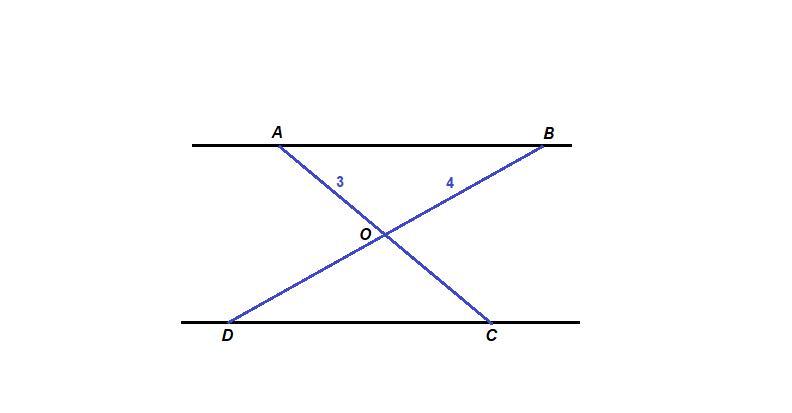
Дано: AB∥CD, OB=4 см, BD=8 см, OA=3 см. Знайти: AC.
А. 1023 см. Б. 6 см. В. 9 см. Г. 7 см.

Ответ:

Б. 6 см

Объяснение:

∠ОАВ = ∠OCD как накрест лежащие при пересечении параллельных прямых АВ и CD секущей АС,

∠АОВ = ∠COD как вертикальные, значит

ΔOAB ~ ΔOCD по двум углам.

OD = BD - OB = 8 - 4 = 4 см

  см

AC = OA + OC = 3 + 3 = 6 см