Математика, вопрос задал Hatio , 1 год назад

Данные выражения равны какому-то постоянному числу. Не делая каких-либо преобразований, примерно определите это постоянное число. Затем, тождественно преобразуя выражения, проверьте верность вашего предположения.

Приложения:

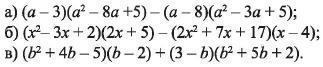
Ответы на вопрос

Ответил Аноним

а) предположим, что все множители с неизвестными x сократятся, и останется число -3·5-(-8)·5 = -15+40 = 25. Проверим:

$(a-3)(a^2-8a+5)-(a-8)(a^2-3a+5)=\\=a^3-8a^2+5a-3a^2+24a-15-(a^3-3a^2+5a-8a^2+24a-40)=\\=a^3-11a^2+29a-15-a^3+11a^2-29a+40=-15+40=25$

Предположение было верным.

б) Аналогично: все множители с неизвестными x сократятся, останется число 2·5-17·(-4) = 10+68 = 78:

$(x^2-3x+2)(2x+5)-(2x^2+7x+17)(x-4)=\\=2x^3+5x^2-6x^2-15x+4x+10-(2x^3-8x^2+7x^2-28x+17x-68)=\\=2x^3-x^2-11x+10-2x^3+x^2+11x+68=10+68=78$

Предположение было верным.

в) все множители с неизвестными b сократятся, останется число (-5)·(-2)+3·2 = 10+6 = 16:

$(b^2+4b-5)(b-2)+(3-b)(b^2+5b+2)=\\=b^3-2b^2+4b^2-8b-5b+10+3b^2+15b+6-b^3-5b^2-2b=\\=b^3+2b^2-13b+10-b^3-2b^2+13b+6=10+6=16$

Предположение было верным.

Новые вопросы

Математика, 1 год назад

Химия, 1 год назад

Физика, 1 год назад

Алгебра, 1 год назад

Алгебра, 6 лет назад

Алгебра, 6 лет назад